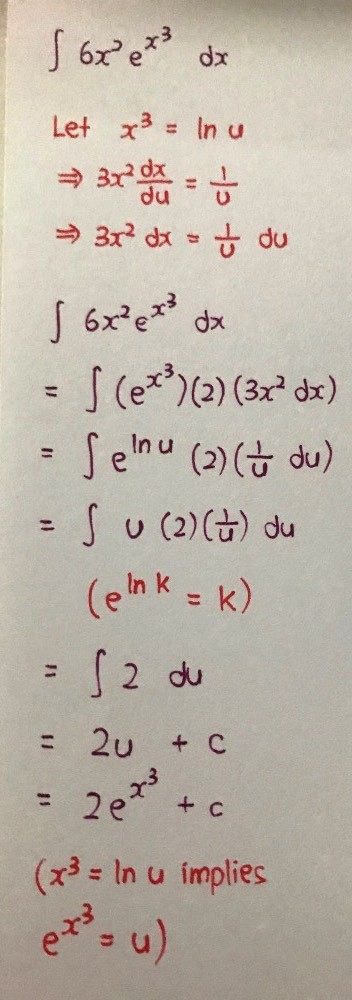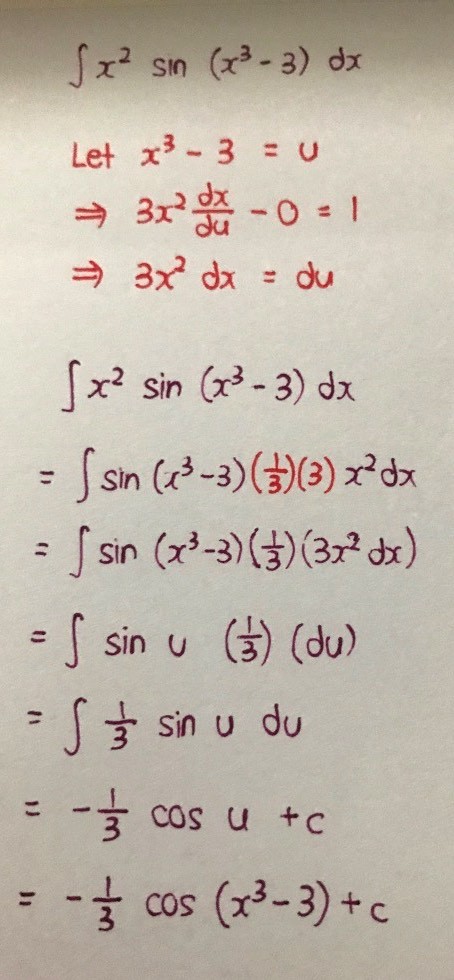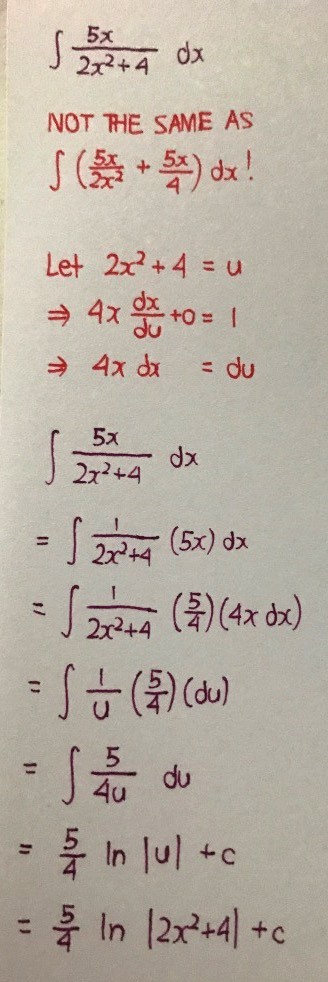Hi guys jus take note first qns e power of x, x is the power of 3 that 3 hard to see so yah

The three parts are much better done using a reverse of the chain rule than by substitution.

Uhh i see bt the qns want in sub method so isit hard that way?

The first term is 6x^2 times e^(x^3).

Observe that differentiating x^3 gives us 3x^2, which is a constant multiple of 6x^2.

If you have done differentiation before, if we were to differentiate e^(x^3), we would get e^(x^3) times d/dx (x^3)...

...where the d/dx (x^3) = 3x^2 is our chain.

So, done in reverse, integrating 3x^2 * e^(x^3) is e^(x^3) + c.

Therefore, integrating the integral in part a, we get 2e^(x^3) + c.

This is why I made mention of the "reverse-chain".

Substitution is more difficult, and I can think of what substitutions to use.

Perhaps the first one can use some ln expression (like x^3) = ln u, but I am not 100% sure.

Second one maybe is using u = x^3 - 3.

Third one, the toughest, requires me to convert 2x^2 to 4 tan^2 x so that I can simplify the denominator using the identity tan^2 x + 1 = sec^2 x.

Having said that, the reverse chain idea is more straightforward as all three questions are capable of being done this way.

Uhh i see that helps thank