Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | E Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Pls help as soon as possible
See 1 Answer
Part a is just plain subbing in of x = 6 and rounding off to 2 decimal places to follow the other data values.
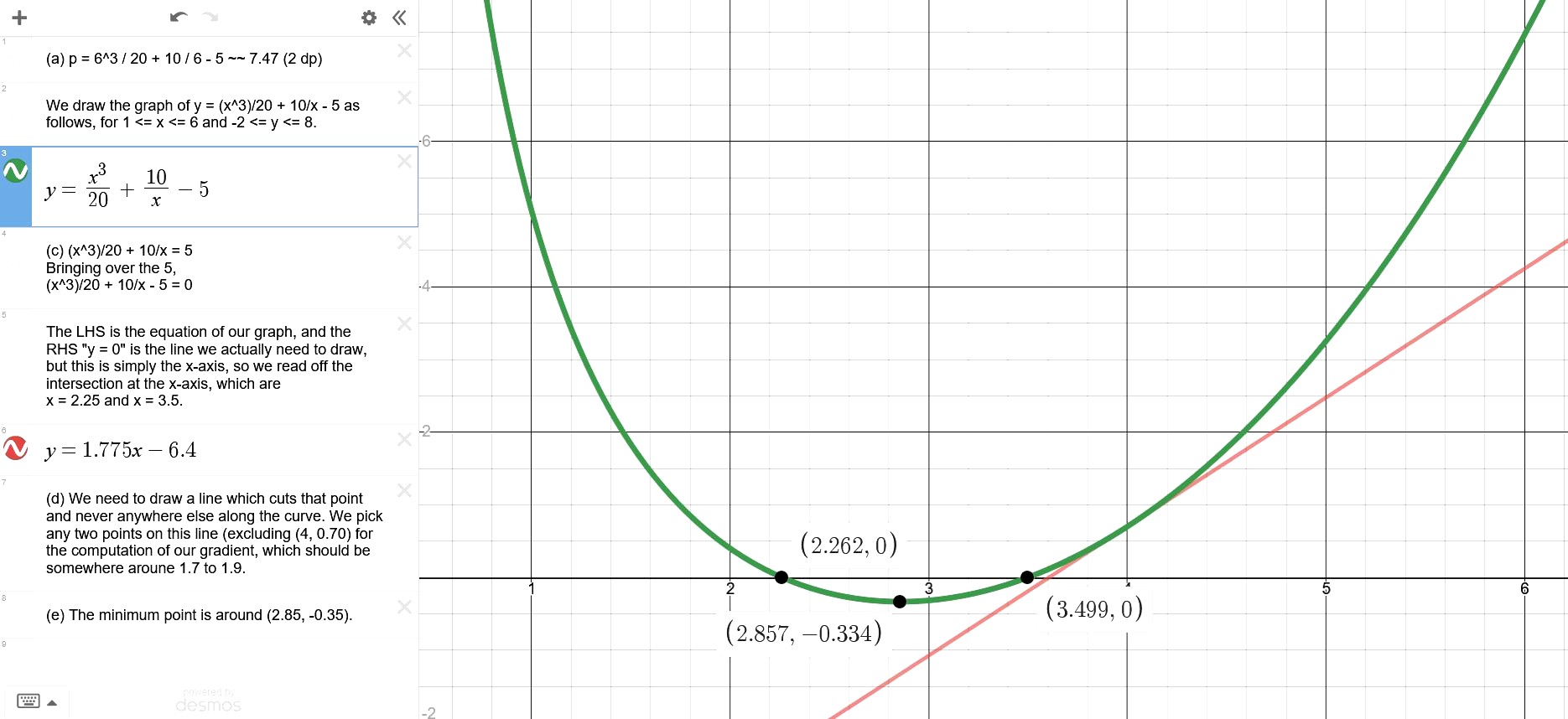
Part b you will need to come up with your own axes and data plotting. You may wish to add additional points on your own to improve the accuracy of your graph, perhaps at the x = 0.5, 1.5, 2.5, 3.5, 4.5 and 5.5 mark.
Part (c), after some rearranging, is just asking us to find the x-coordinates of intersection between the curve and the x-axis.
Part (d) is for us to draw a tangent to the curve at (4, 0.70). I actually "cheated" by using dy/dx and forming the equation of the tangent myself (which obviously you know how to do as well) to have a rough idea of the gradient of the line to draw. This is to ensure that my gradient is not too far off the actual value, because accuracy marks can be lost here.
Part (e) is for us to locate and read off the coordinates of the minimum point. There is no need to do dy/dx here as the turning point should be quite accurately located if you have drawn the graph well.
Let me know if you need more explanation.