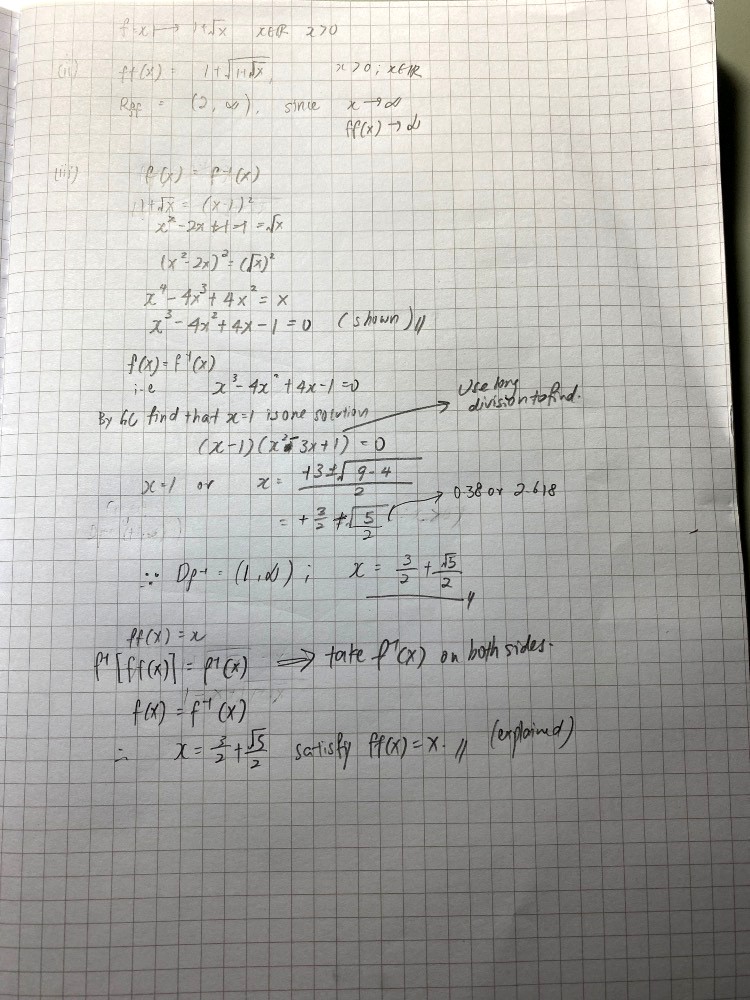f(x) = 1 + √x

Replace f(x) with x and x with f-¹(x),

x = 1 + √f-¹(x)

x - 1 = √f-¹(x)

(x - 1)² = f-¹(x)

f-¹(x) = (x - 1)²

Domain of f-¹ = range of f = (1,∞)

ff(x)

= f(1 + √x)

= 1 + √(1 + √x)

The domain of ff is a subset of the range of f = (1,∞)

When x = 1 ,

ff(x) = 1 + √(1 + √1)

= 1 + √2

As x → ∞, √x →∞ . So do 1 + √x and √(1 + √x)

So 1 + √(1 + √x) → ∞ as well

Range of ff = (1 + √2, ∞)

When f(x) = f-¹(x) ,

1 + √x = (x - 1)²

√x = (x - 1)² - 1 = x² - 2x + 1 - 1 = x² - 2x

x = (x² - 2x)²

x = x⁴ - 4x³ + 4x²

x⁴ - 4x³ + 4x² - x = 0

x(x³ - 4x² + 4x - 1) = 0

x = 0 or x³ - 4x² + 4x - 1 = 0 (shown)
(Rejected as x > 0 for f(x) as defined)

x³ - 4x² + 4x - 1 = 0

Sub x = 1 , f(1) = 1³ - 4(1²) + 4(1) - 1 = 0

By the factor theorem, (x - 1) is a factor.

(x - 1)(x² - 3x + 1) = 0
x = 1 or x² - 3x + 1 = 0

(x = 1 is rejected as x > 1 for f-¹(x) as defined)

x² - 2(3/2)x + (3/2)² - (3/2)² + 1 = 0
(x - 3/2)² = 5/4

x - 3/2 = ±√(5/4)

x = 3/2 + √5/2 or x = 3/2 - √5/2 (rejected as x > 1 for f-¹(x) as defined

so x = 3/2 + √5/2 or ½(3 + √5)

This value satisfies f-¹(x) = f(x).

When f(x) = f-¹(x), ff(x) = ff-¹(x) = x

So this value will satisfy the equation ff(x) = x

(In other words, when f(x) = f-¹(x), ff(x) = x)

Sorry for the late response, but thank you so much!! :)

Welcome