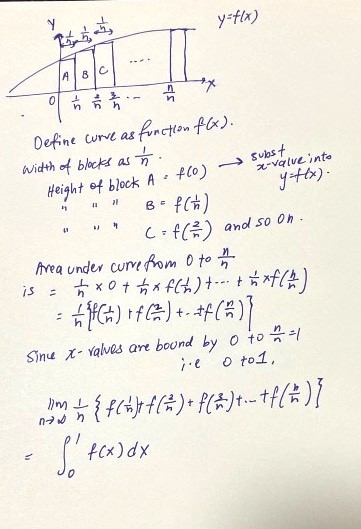Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 1 | H2 Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

Help please!
The height of each rectangle is f(a/n), it's the y value you obtain.
a represents the particular division each rectangle is at.
See 2 Answers
You have to
(1) define the width of rectangular blocks under the curve f(x) as 1/n
(2) you have to find the height of each block by substituting the values of x into f(x). The values of the heights are f(1/n), f(2/n)... f(n/n); look at the graph drawn to better understand what I mean.
(3) Thereafter the area under curve can be found by adding all the rectangular blocks with width (1/n) and height which corresponds to the x value.
Examine and conclude that the bigger the value of n, the smaller the value of 1/n which makes the approx of the area more accurate since you can squeeze in more of these “rectangular blocks”.
You will then come to the same equation given in the question. Thereafter, you must be able to derive what what the value of limit n to infinity of {f(1/n)+f(2/n)+...+f(n/n)}.
Think through; 1/n if n is infinity is near 0 (e.g 0.00000000000000000000000000000000001) and so is 2/n and 3/n and so on. n/n when n is huge is 1. Therefore limiting n to infinity for the addition becomes slightly over 1 or just 1 since the decimal is negligible when n is huge if it makes sense.
Looking at the graph since the blocks start at 0 and nears to 1 the area of the curve can be written as the form given.
Part (II) requires a derivation of what f(x) is. As per mentioned earlier, f(1/n) f(2/n) etc is just substituting x values into f(x) therefore if we swap out 1/n with x will give us the original f(x) which is cuberoot x^3.
Part (I) tests the concept of integration.
You have to
(1) define the width of rectangular blocks under the curve f(x) as 1/n
(2) you have to find the height of each block by substituting the values of x into f(x). The values of the heights are f(1/n), f(2/n)... f(n/n); look at the graph drawn to better understand what I mean.
(3) Thereafter the area under curve can be found by adding all the rectangular blocks with width (1/n) and height which corresponds to the x value.
Examine and conclude that the bigger the value of n, the smaller the value of 1/n which makes the approx of the area more accurate since you can squeeze in more of these “rectangular blocks” which is what the limit n to infinity means. Don’t have to fret it’s not asking you to derive x values from this complex eqn.
You will then come to the same equation given in the question.
***Correction here: To find the x-bound for the area of curve, just look at the start and end. The start of the x value should be 1/n and if we limit n to infinity 1/n becomes very small and negligible ie 0 and n/n still becomes 1 which is why the integration is between x=0 and x=1. Ignore what is written in the box on the right of the graph.
Looking at the graph since the blocks is from 0
Part (II) requires a derivation of what f(x) is. As per mentioned earlier, f(1/n) f(2/n) etc is just substituting x values into f(x) therefore if we swap out 1/n with x will give us the original f(x) which is cuberoot x^3.