Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
junior college 2 | H2 Maths
3 Answers Below
Anyone can contribute an answer, even non-tutors.
Hi’ Can someone pls help me with this questio? Thanks so much:)
Date Posted: 4 years ago
Views: 263
Good evening Sonia! I will look at this later if no one has done them yet.
See 3 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good evening Sonia! Here are my workings for this question. We simply use graphing calculator or some other good calculator to solve the system of four simultaneous equations in four unknowns (I doubt Casio FX 96 SG Plus is capable of doing 4 by 4), since we receive no bonus marks for working out the solutions manually.
Date Posted:
4 years ago
well done
Hi:) Thank u for helping again, can i ask
How do you know that the graph of f(|x|) must pass through (3,25) but the graph of f|(x)| must pass through BOTH (-1,7) and (-1,-7) ?
I’m slightly confused:/
How do you know that the graph of f(|x|) must pass through (3,25) but the graph of f|(x)| must pass through BOTH (-1,7) and (-1,-7) ?
I’m slightly confused:/
Good morning Sonia! My explanation will be very long, and I will simplify it upon your request. This one will be for y = f(|x|), and you can jump to the summary if you find it too long.
--------------------------------------------------------
Whenever we see the expression |something|, it means that anything which comes out of it must be positive. The "something" itself, however, can be positive or negative.
Now, for f(x) and its corresponding f(|x|) where the |x| lies inside f, the function goes this way.
f(|3|) is the same as f(3) because |3| = 3.
f(|2|) is the same as f(2) because |2| = 2.
f(|1|) is the same as f(1) because |1| = 1.
f(|0|) is the same as f(0) because |0| = 0.
f(|-1|) is the same as f(1) because |-1| = 1.
f(|-2|) is the same as f(2) because |-2| = 2.
f(|-3|) is the same as f(3) because |-3| = 3.
Then, where would be see f(-1), f(-2), f(-3) and so on? The thing is, our above results only get us f(positive number). In terms of the original function f(|x|), there is no f(negative).
What this means is that if the graph of f(x) is drawn and we wish to draw the graph of f(|x|), the right half of the graph is retained.
However, since f(-1), f(-2), f(-3),... is seen in the original graph but NOT in the f(|x|) graph (we can never obtain f(negative) out of f(|x|) at all), the left half of the old graph is, well...
...gone! So, the left half of the original graph does not exist in the graph of f(|x|). Instead, we see that for the output results,
f(|3|) = f(|-3|) = f(3)
f(|2|) = f(|-2|) = f(2)
f(|1|) = f(|-1|) = f(1)
f(|0|) = f(|-0|) = f(0)
What we mean by f(|3|) = f(|-3|) is that let's say f(3) = 5, in other words the original graph of f(x) passes through (3, 5). Then f(|3|) and f(|-3|) both simply to f(3) which equals 5, so f(|3|) = f(|-3|) = 5. In other words, the graph of f(|x|) passes through both (3, 5) AND (-3, 5).
Similarly, if the graph of f(x) passes through (2, 3), then f(|2|) and f(|-2|) both simply to f(2) which equals 3, so f(|2|) = f(|-2|) = 3. In other words, the graph of f{|x|) passes through both (2, 3) AND (-2, 3).
The same idea goes for f(|1|) and f(|-1|) and for other pairs of points.
What this means is that the left half, which was previously discarded, is now replaced by a graph which is an exact reflection of the right side of the graph along the y-axis. This is because f(|1|) = f(|-1|), f(|2|) = f(|-2|), f(|3|) = f(|-3|) and so on, meaning that points equally far from the y-axis are at the same height level.
--------------------------------------------------------
In summary, for the graph of f|x|), what we do is this.
From the graph of f(x),
- retain the right half of the graph
- discard the left half of the graph and replace it by a graph equal to the reflection of the right half of the graph along the y-axis
y = |x| is a very good example of this which you have learnt two years ago in Sec 3. Observe that when we compare the graphs of y = x and y = |x|, we see that the right half of the original graph y = x is retained while the left half is discarded and replaced with something which looks like a reflection of the right hand side about the y-axis (coincidentally for this particular graph, it is also a reflection along the x-axis which you learnt two years ago, but this "reflection along the x-axis" is not true in general for f(|x|)).
--------------------------------------------------------
So, the graph of y = f(|x|) has a line of symmetry along the y-axis. This is why by converse reasoning of my long explanation above, if the graph passes through (-3, 25), it must ALSO passes through (3, 25). The original graph y = f(x), however, did not have the left half of the graph as such. So, the original graph y = f(x) may not pass through (-3, 25) but it must pass through (3, 25).
So, for our equation f(x) = ax^3 + bx^2 + cx + d, we cannot use (-3, 25) as our coordinates, but we can use (3, 25) as our coordinates.
--------------------------------------------------------
Whenever we see the expression |something|, it means that anything which comes out of it must be positive. The "something" itself, however, can be positive or negative.
Now, for f(x) and its corresponding f(|x|) where the |x| lies inside f, the function goes this way.
f(|3|) is the same as f(3) because |3| = 3.
f(|2|) is the same as f(2) because |2| = 2.
f(|1|) is the same as f(1) because |1| = 1.
f(|0|) is the same as f(0) because |0| = 0.
f(|-1|) is the same as f(1) because |-1| = 1.
f(|-2|) is the same as f(2) because |-2| = 2.
f(|-3|) is the same as f(3) because |-3| = 3.
Then, where would be see f(-1), f(-2), f(-3) and so on? The thing is, our above results only get us f(positive number). In terms of the original function f(|x|), there is no f(negative).
What this means is that if the graph of f(x) is drawn and we wish to draw the graph of f(|x|), the right half of the graph is retained.
However, since f(-1), f(-2), f(-3),... is seen in the original graph but NOT in the f(|x|) graph (we can never obtain f(negative) out of f(|x|) at all), the left half of the old graph is, well...
...gone! So, the left half of the original graph does not exist in the graph of f(|x|). Instead, we see that for the output results,
f(|3|) = f(|-3|) = f(3)
f(|2|) = f(|-2|) = f(2)
f(|1|) = f(|-1|) = f(1)
f(|0|) = f(|-0|) = f(0)
What we mean by f(|3|) = f(|-3|) is that let's say f(3) = 5, in other words the original graph of f(x) passes through (3, 5). Then f(|3|) and f(|-3|) both simply to f(3) which equals 5, so f(|3|) = f(|-3|) = 5. In other words, the graph of f(|x|) passes through both (3, 5) AND (-3, 5).
Similarly, if the graph of f(x) passes through (2, 3), then f(|2|) and f(|-2|) both simply to f(2) which equals 3, so f(|2|) = f(|-2|) = 3. In other words, the graph of f{|x|) passes through both (2, 3) AND (-2, 3).
The same idea goes for f(|1|) and f(|-1|) and for other pairs of points.
What this means is that the left half, which was previously discarded, is now replaced by a graph which is an exact reflection of the right side of the graph along the y-axis. This is because f(|1|) = f(|-1|), f(|2|) = f(|-2|), f(|3|) = f(|-3|) and so on, meaning that points equally far from the y-axis are at the same height level.
--------------------------------------------------------
In summary, for the graph of f|x|), what we do is this.
From the graph of f(x),
- retain the right half of the graph
- discard the left half of the graph and replace it by a graph equal to the reflection of the right half of the graph along the y-axis
y = |x| is a very good example of this which you have learnt two years ago in Sec 3. Observe that when we compare the graphs of y = x and y = |x|, we see that the right half of the original graph y = x is retained while the left half is discarded and replaced with something which looks like a reflection of the right hand side about the y-axis (coincidentally for this particular graph, it is also a reflection along the x-axis which you learnt two years ago, but this "reflection along the x-axis" is not true in general for f(|x|)).
--------------------------------------------------------
So, the graph of y = f(|x|) has a line of symmetry along the y-axis. This is why by converse reasoning of my long explanation above, if the graph passes through (-3, 25), it must ALSO passes through (3, 25). The original graph y = f(x), however, did not have the left half of the graph as such. So, the original graph y = f(x) may not pass through (-3, 25) but it must pass through (3, 25).
So, for our equation f(x) = ax^3 + bx^2 + cx + d, we cannot use (-3, 25) as our coordinates, but we can use (3, 25) as our coordinates.
Instead, for the graph of |f(x)|, this is simply an entire modulus of the entire f(x) graph, which you have already learnt two years ago. This time, the reflection is done along the x-axis, so any portion of the graph which is below the x-axis gets reflected upwards.
If a point is previously as (2, 4), then the new position in y = |f(x)| will still be at (2, 4), because 4 is positive. However, if a point is previously at (2, -4), then the new position in y = |f(x)| is going to be at (2, 4), because -4 is negative and |f(x)| represents |y|, or |-4|, which is 4.
This is why by converse reasoning, if the graph of y = |f(x)| passes through (-1, 7), the original graph y = f(x) can pass through EITHER one of the following, but NOT BOTH at the same time.
- The original graph may pass through (-1, 7).
- The original graph may pass through (-1, -7).
We list this down as separate cases as we attempt to obtain our values for a, b, c and d.
-----------------------------------------------------
In summary,
- for f(x) to f(|x|), discard the left portion and replace it by a reflection of the right portion along the x-axis
- for f(x)to |f(x)|, reflect any portion below the x-axis to above the x-axis (and of course discard the portion below the x-axis afterwards)
Sonia, let me know if you are still confused and I will explain them again.
If a point is previously as (2, 4), then the new position in y = |f(x)| will still be at (2, 4), because 4 is positive. However, if a point is previously at (2, -4), then the new position in y = |f(x)| is going to be at (2, 4), because -4 is negative and |f(x)| represents |y|, or |-4|, which is 4.
This is why by converse reasoning, if the graph of y = |f(x)| passes through (-1, 7), the original graph y = f(x) can pass through EITHER one of the following, but NOT BOTH at the same time.
- The original graph may pass through (-1, 7).
- The original graph may pass through (-1, -7).
We list this down as separate cases as we attempt to obtain our values for a, b, c and d.
-----------------------------------------------------
In summary,
- for f(x) to f(|x|), discard the left portion and replace it by a reflection of the right portion along the x-axis
- for f(x)to |f(x)|, reflect any portion below the x-axis to above the x-axis (and of course discard the portion below the x-axis afterwards)
Sonia, let me know if you are still confused and I will explain them again.
Also, on a separate note unrelated to the moduluses, before I forget.
For the graph y = ax^3 + bx^2 + cx + d, if the graph has a minimum point to the left of the maximum point, then the coefficient of x^3, a, must be negative, and similarly, if the graph has a maximum point to the left of the minimum point, then a must be positive. This applies to such x^3 graphs which possess both maximum and minimum points (not all cubic graphs have stationary points).
For the graph y = ax^3 + bx^2 + cx + d, if the graph has a minimum point to the left of the maximum point, then the coefficient of x^3, a, must be negative, and similarly, if the graph has a maximum point to the left of the minimum point, then a must be positive. This applies to such x^3 graphs which possess both maximum and minimum points (not all cubic graphs have stationary points).
Thank u! Can i clarify how come there’s no equation from the graph that pass through (-3,25)?
Because all the left portion of the graph f(|x|) is actually a reflection of the right hand side. Prior to this, there was nothing on the left portion at all because that portion of y = f(x) was eliminated.
The (-3, 25) is a point on this f(|x|) graph, all because of the reflection. The original graph did not contain this point.
In other words, the graph of f(|x|) has that point (-3, 25), but the original graph of f(x) did not have this point.
Hence, we cannot substitute (-3, 25) into the expression for f(x).
The (-3, 25) is a point on this f(|x|) graph, all because of the reflection. The original graph did not contain this point.
In other words, the graph of f(|x|) has that point (-3, 25), but the original graph of f(x) did not have this point.
Hence, we cannot substitute (-3, 25) into the expression for f(x).
Thank u!:-))
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
ye :)
Date Posted:
4 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
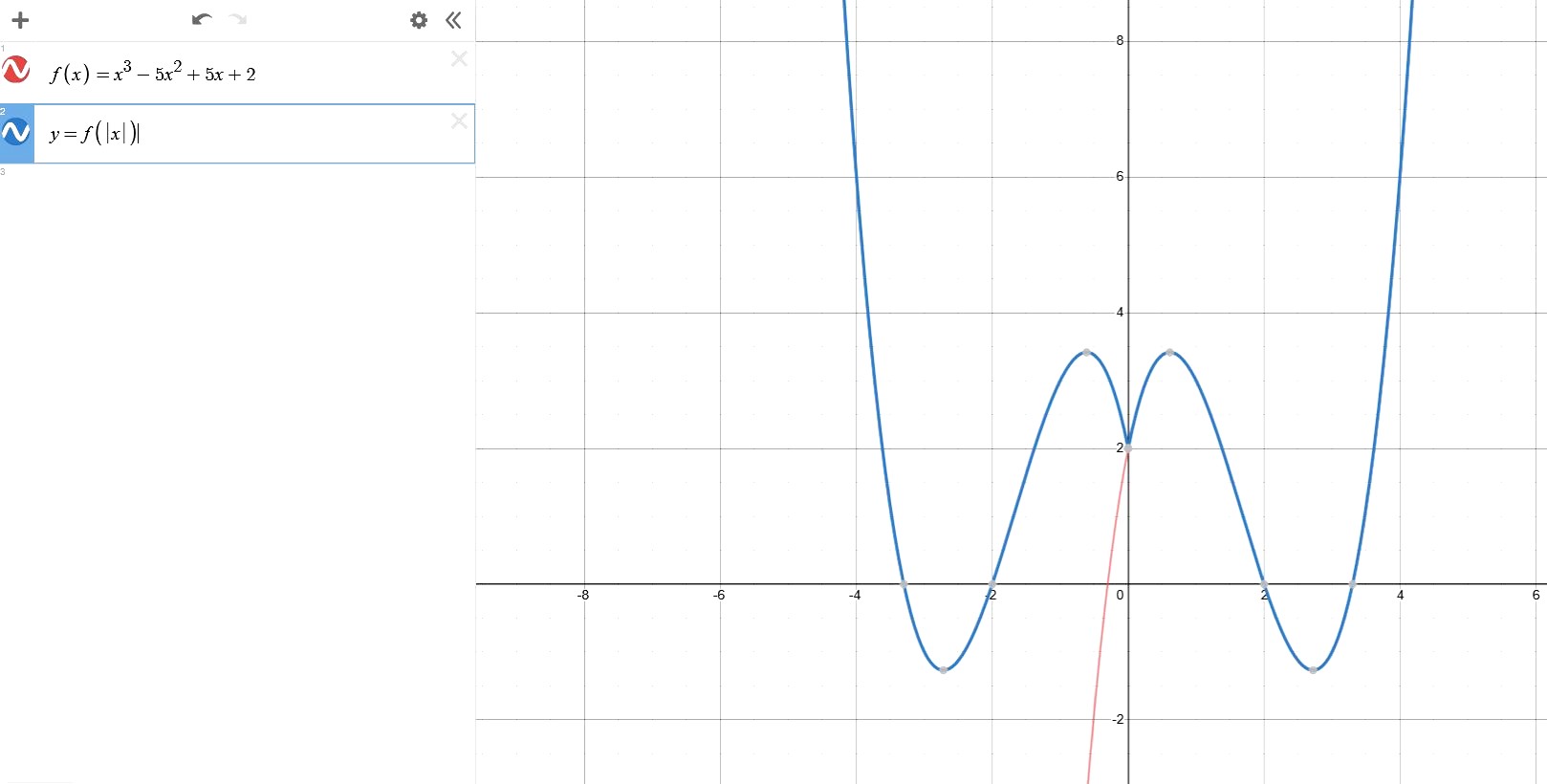
Sonia, here is an illustration for the graph of y = f(x) = x^3 - 5x^2 - 5x + 3 and the corresponding graph y = f(|x|). Observe that the right half of the red (original) graph overlaps with the new f(|x|) graph, whereas the left hand of the red graph is discarded, and taking its place is a reflected graph. The line of symmetry is the y-axis itself.
Date Posted:
4 years ago
360 Tutoring Program