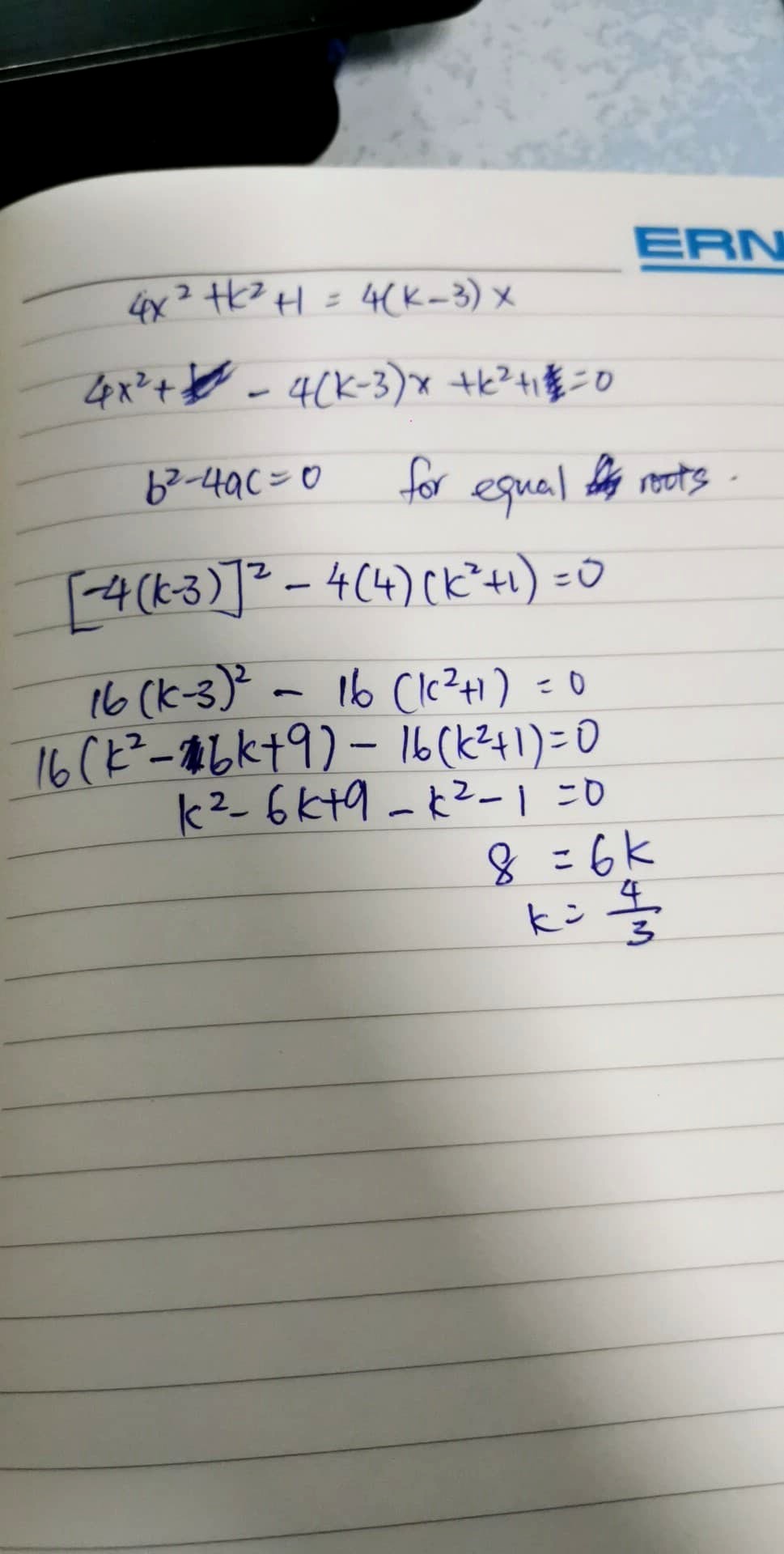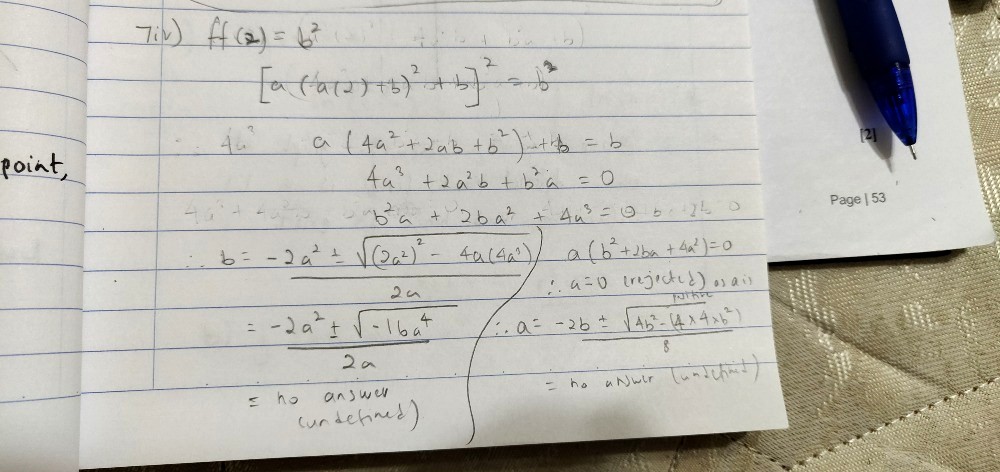Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 1 | H2 Maths
3 Answers Below
Anyone can contribute an answer, even non-tutors.

How to do part 3 and 4 (iii and iv)?
f(2) = (a(2) + b)² = (2a + b)²
When ff(2) = b²,
(a(2a+b)² + b)² = b²
(a(2a + b)² + b)² - b² = 0
(a(2a + b)² + b - b)(a(2a + b)² + b + b) = 0
a(2a + b) = 0 or a(2a + b)² + 2b = 0
a = 0 or b = -2a
or
4a³ + 4a²b + ab² + 2b = 0
ab² + (4a² + 2)b + 4a³ = 0
b = [-(4a² + 2)± √( (4a² + 2)² - 4(a)(4a³) ) ] / 2a
b = [-(4a² + 2) ± √(16a⁴ + 16a² + 4 - 16a⁴)] / 2a
b = [-(4a² + 2) ± √(16a² + 4) ] / 2a
b = [-(4a² + 2) ± 2√(4a² + 1)] / 2a
b = -2a - [1± √(4a² + 1)] / a
See 3 Answers

The answer key says no answer
Can don’t be A if it’s confusing can be C/D/E/F etc.
The part 3 I can understand though.
“Given ff(x)=b^2” and
“let A=(ax+b)^2”
If still cannot understand, I’ll post the workings.