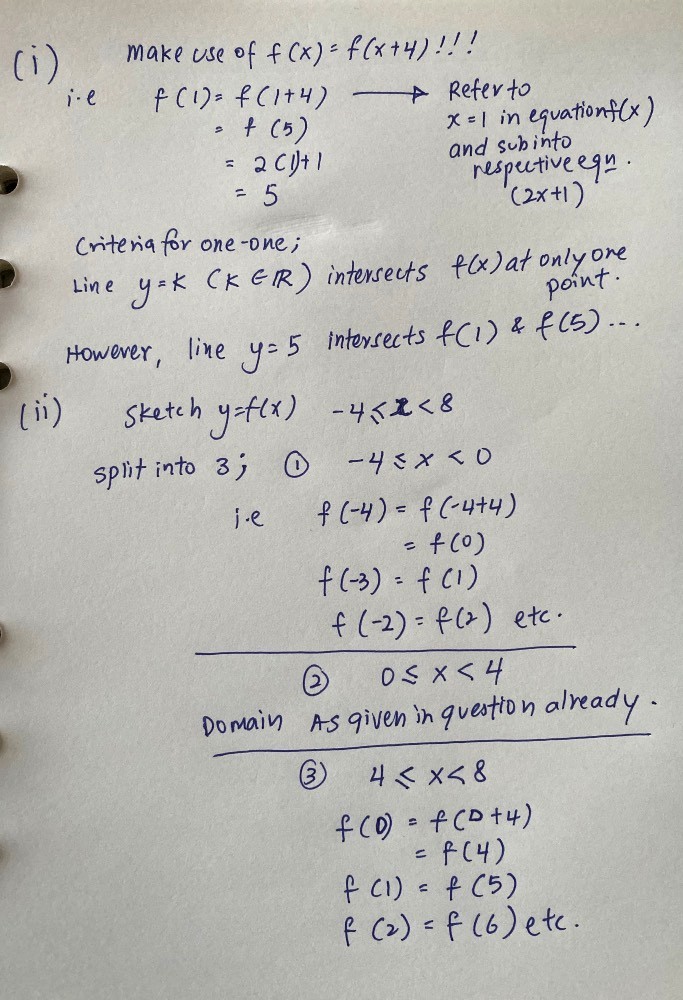f(1) = 2(1) + 1 = 3

f(5) = f(1 + 4) = f(1) = 3 (since f(x) = f(x + 4) )

For a function f to be one-one, every value of f(x) must correspond to only 1 value of x.

Since f(x) = f(x + 4) , then a certain value of f(x) will correspond to more than 1 value of x so it is not one-one

For the above example, f(x) = 4 when x = 1 and when x = 5 (and also when x = 9,13,17,21...and so on)

ii)

We know f(x) = f(x+4)

So the portion of the function where the domain is 0 ≤ x < 2, is the same as the portion for 0 ≤ x + 4 < 2 ,

which in turn gives -4 ≤ x < -2

So for the two portions where 0 ≤ x < 2 and -4 ≤ x < -2, you draw f(x) = 2x + 1

Now, if 0 ≤ x < 2, then 4 ≤ x + 4 < 6

Since f(x) = f(x + 4), then this portion of the graph is also the same as for 4 ≤ x < 6 .

So you also draw f(x) = 2x + 1 for 4 ≤ x < 6 .


Likewise,

the portion of the function where the domain is 2 ≤ x < 4 is the same as the portion for 2 ≤ x + 4 < 4 ,

which in turn gives -2 ≤ x < 0

So for the two portions where 2 ≤ x < 4 and -2 ≤ x < 0, you draw f(x) = (x-4)² +1

Now, if 2 ≤ x < 4, then 6 ≤ x + 4 < 8

Since f(x) = f(x + 4), then this portion of the graph is also the same as for 6 ≤ x < 8 .

So you also draw f(x) = (x - 4)² + 1 for 6 ≤ x < 8 .


Basically, the portions repeat every 4 units on the x-axis.

To summarise :

-4 ≤ x < -2 : f(x) = 2x + 1

-2 ≤ x < 0 : f(x) = (x - 4)² + 1

0 ≤ x < 2 : f(x) = 2x + 1

2 ≤ x < 4 : f(x) = (x - 4)² + 1

4 ≤ x < 6 : f(x) = 2x + 1

6 ≤ x < 8 : f(x) = (x - 4)² + 1

Ohhh thank you so much!!! :)

Welcome. Part iii) should be easy. ［1,5]

One more thing to note :

Do not use the actual x values to compute f(x) for the other 4 subdomains. Draw the graph for 0 ≤ x < 2 and 2 ≤ x < 4 . Then replicate each of these portions for the corresponding subdomains.