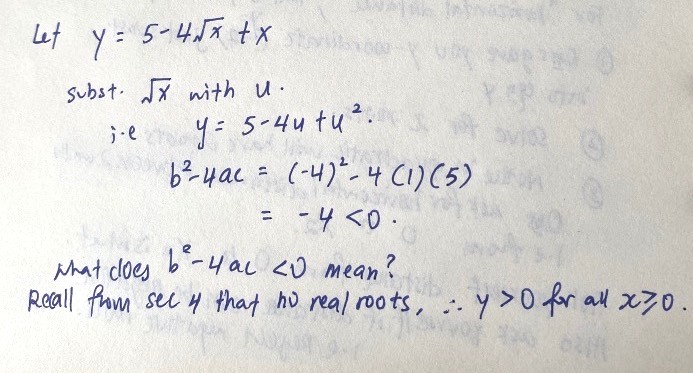Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 2 | H2 Maths
3 Answers Below
Anyone can contribute an answer, even non-tutors.

Hello! Please help me with this qns for both parts:-)
I can’t do the first part when i replace x with u^2 and root x with u ..
for eg. 5-4rootx+x =0
5-4u+u^2=0
*no solution*
so i don’t know how to continue.
Thanks so much
= (√x)² - 2(2√x) + 2² + 1
= (√x - 2)² + 1
For all x ≥ 0, √x is a real number and √x ≥ 0
(√x - 2)² also ≥ 0 since √x - 2 is also a real number and the square of a real number is always 0 or positive.
So (√x - 2)² + 1 ≥ 1 > 0
Which means that (√x - 1)² > 0
Thus 5 - 4√x + x > 0 for all x ≥ 0
See 3 Answers
In fact, this approach I have done now can be used for quadratic inequalities as well! Except that you learnt to draw a quadratic curve for the quadratic inequality when you learnt them two years ago.
Here, we must be careful with the inequality as the presence of the square root means that x cannot be negative as well.
Sonia, let me know if you need more explanation.