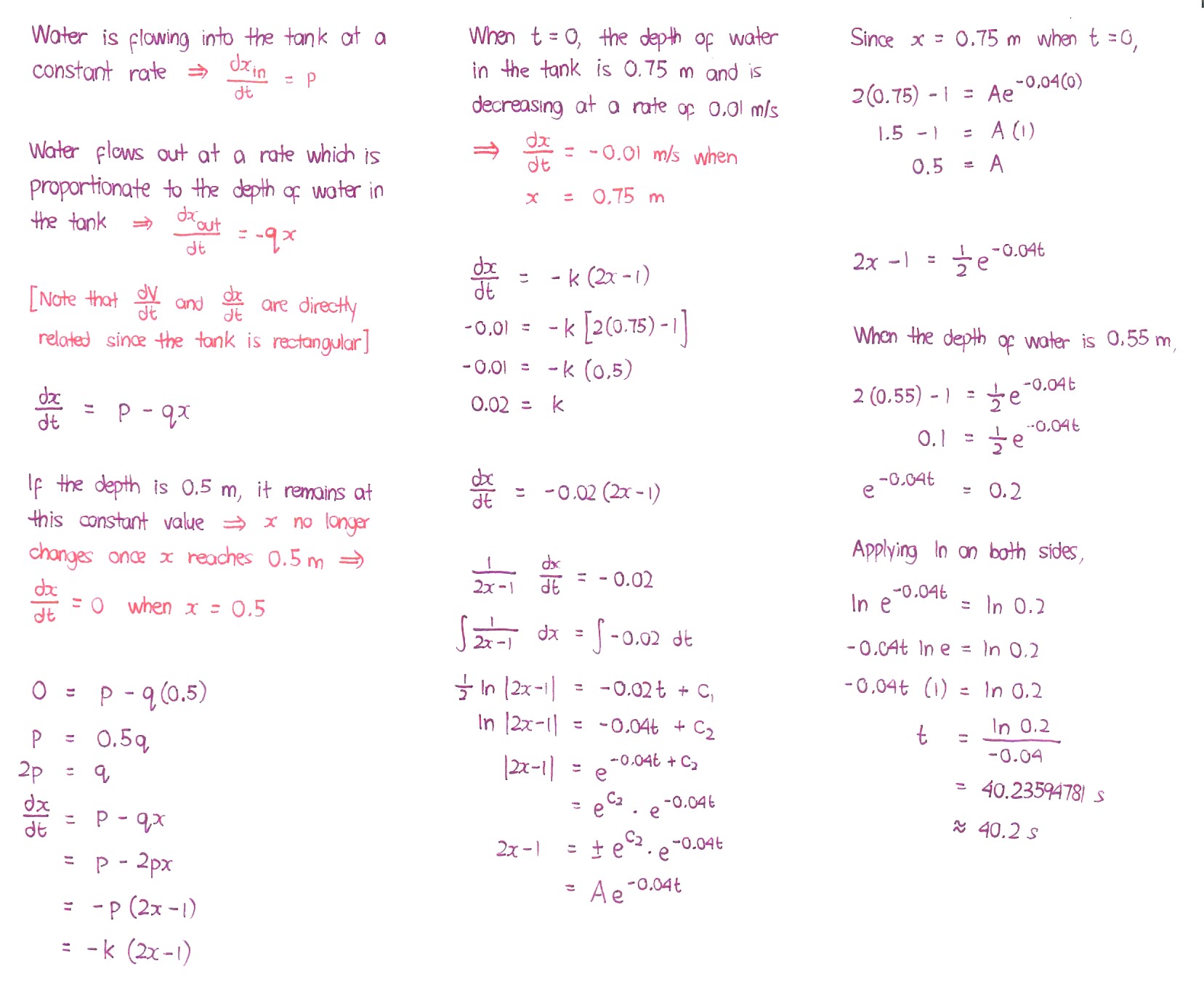Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

See 2 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good evening Janet! Here are my workings for the proving part. I will do the remaining when I am less tired.
Date Posted:
4 years ago
Good afternoon Janet! The forum system was down at 2 am and my completed answer could not get sent in as a result. I will send the remaining part to you tonight.
I just tried to submit again on several occasions but could not get my workings sent in successfully.
I will type my workings here instead temporarily.
We obtain dx/dt = -k (2x - 1).
------------------------------------------------
Now, when t = 0, the depth of water in the tank is 0.75 m and is decreasing at a rate of 0.01 m/s.
This means that, dx/dt = -0.01 when x = 0.75.
Let's substitute this into the above equation.
dx/dt = -k (2x - 1)
-0.01 = -k [2 (0.75) - 1]
-0.01 = -0.5k
k = 0.02
dx/dt = -0.02 (2x - 1)
1/(2x - 1) dx/dt = -0.02
Integrating both sides,
INT [1/(2x - 1)] dx = INT (-0.02) dt
We then have
0.5 ln |2x - 1| = -0.02t + c1
ln |2x - 1| = -0.04t + c2
Removing ln,
|2x - 1| = e^[-0.04t + c2]
|2x - 1| = e^c2 * e^(-0.04t)
Removing the modulus,
2x - 1 = +- e^c2 * e^(-0.04t)
2x - 1 = Ae^-0.04t
where I used A to denote the constant +- e^c2.
Now, at this point, we are almost done. We need to obtain the value of A. Since x = 0.75 when t = 0,
2 (0.75) - 1 = Ae^(-0.04 * 0)
1.5 - 1 = Ae^0
A = 0.5
2x - 1 = 0.5 e^(-0.04t)
When the depth of the water is 0.55 m.
2 (0.55) - 1 = 0.5 e^(-0.04t)
0.1 = 0.5 e^(-0.04t)
e^(-0.04t) = 0.2
Applying ln on both sides,
ln e^(-0.04t) = ln 0.2
(-0.04t) ln e = ln 0.2
(-0.04t) (1) = ln 0.2
-0.04t = ln 0.2
Finally,
t = (ln 0.2) / (-0.04)
t = 40.23594781 s
t ~ 40.2 s
We obtain dx/dt = -k (2x - 1).
------------------------------------------------
Now, when t = 0, the depth of water in the tank is 0.75 m and is decreasing at a rate of 0.01 m/s.
This means that, dx/dt = -0.01 when x = 0.75.
Let's substitute this into the above equation.
dx/dt = -k (2x - 1)
-0.01 = -k [2 (0.75) - 1]
-0.01 = -0.5k
k = 0.02
dx/dt = -0.02 (2x - 1)
1/(2x - 1) dx/dt = -0.02
Integrating both sides,
INT [1/(2x - 1)] dx = INT (-0.02) dt
We then have
0.5 ln |2x - 1| = -0.02t + c1
ln |2x - 1| = -0.04t + c2
Removing ln,
|2x - 1| = e^[-0.04t + c2]
|2x - 1| = e^c2 * e^(-0.04t)
Removing the modulus,
2x - 1 = +- e^c2 * e^(-0.04t)
2x - 1 = Ae^-0.04t
where I used A to denote the constant +- e^c2.
Now, at this point, we are almost done. We need to obtain the value of A. Since x = 0.75 when t = 0,
2 (0.75) - 1 = Ae^(-0.04 * 0)
1.5 - 1 = Ae^0
A = 0.5
2x - 1 = 0.5 e^(-0.04t)
When the depth of the water is 0.55 m.
2 (0.55) - 1 = 0.5 e^(-0.04t)
0.1 = 0.5 e^(-0.04t)
e^(-0.04t) = 0.2
Applying ln on both sides,
ln e^(-0.04t) = ln 0.2
(-0.04t) ln e = ln 0.2
(-0.04t) (1) = ln 0.2
-0.04t = ln 0.2
Finally,
t = (ln 0.2) / (-0.04)
t = 40.23594781 s
t ~ 40.2 s
Thanks
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Good afternoon Janet! Here are my written workings for the question.
Date Posted:
4 years ago