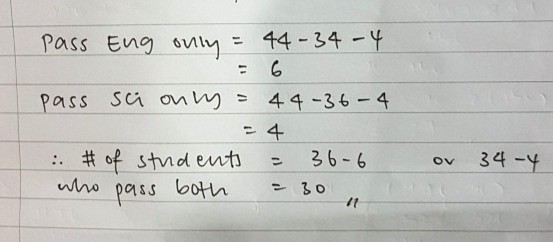40 pupils passed either Science or English or both.

34 pupils passed Science (but we cannot distinguish between pass Science only and pass both) while 36 pupils passed English (but we cannot distinguish between pass English only and pass both).

I will use a little bit of algebra here, but since this is a P5 question, I will try and keep the algebra simple.

We do not know how many pupils passed Science only, how many pupils passed English only and how many pupils passed both subjects.

So, we let the number of pupils who passed both subjects be x.

Now, if 34 pupils passed Science (and x of them also passed English), then there must be (34 - x) pupils who passed Science ONLY.

And if 36 pupils passed English (and x of them also passed Science), then there must be (36 - x) pupils who passed English ONLY.

So putting them together,

Passed Science and English: x
Passed Science only: (34 - x)
Passed English only: (36 - x)

The three cases above account for the 40 people who passed at least one subject.

So, we have

x + (34- x) + (36 - x) = 40
x + 34 - x + 36 - x = 40
34 + 36 + x - x - x = 40
70 - x = 40
x = 30

So 30 pupils passed both subjects (while 4 pupils passed Science only, 6 pupils passed English only and 4 pupils passed neither paper).

Assumption approach for this question is also possible, but complicated.

Now, there are 34 pupils who passed Science while 36 pupils who passed English, but there are only a total of 40 pupils who passed at least one of them.

Assume none of the pupils passed both subjects (so that 34 pupils passed Science only and 36 pupils passed English only). Then there should be 70 pupils altogether, but this is not the case.

Now, assume 1 pupil passed both subjects. This leaves 33 pupils passing Science only and 35 pupils passing English only. Then, there would be 69 pupils altogether in this case.

Now, assume 2 pupils passed both subjects. This leaves 32 pupils passing Science only and 34 pupils passing English only. Then, there would be 68 pupils altogether in this case.

Now, assume 3 pupils passed both subjects. This leaves 31 pupils passing Science only and 33 pupils passing English only. Then, there would be 67 pupils altogether in this case.

And we follow this trend. Observe that for every extra pupil who passed both subjects, the total number of pupils will decrease by 1.

To get from a total of 40 pupils (from the extreme case of 70 pupils), there must clearly be a decrease in the number of pupils by 30.

This means that there must be an increase in the number of pupils who passed both subjects by 30 (from 0 at the start).

So, 30 pupils passed both subjects.

total: 44
fail Sci: 10
fail EL: 8
fail both Sci & EL: 4
so
fail Sci only: 10-4 = 6
fail EL only: 8-4 = 4
hence
no. at least one subj fail: 4+6+4 = 14

no. passed both subj.: 44-14 = 30

.
.
.

Thank you