Good morning Sonia! Not to worry, I will look at your question in a moment!

Idea is that 6 - curve is a maximum when the curve is at its minimum (because the smaller number you choose to subtract, the larger the final number you achieve, for example 6 - 1 = 5 while 6 - 6 = 0).

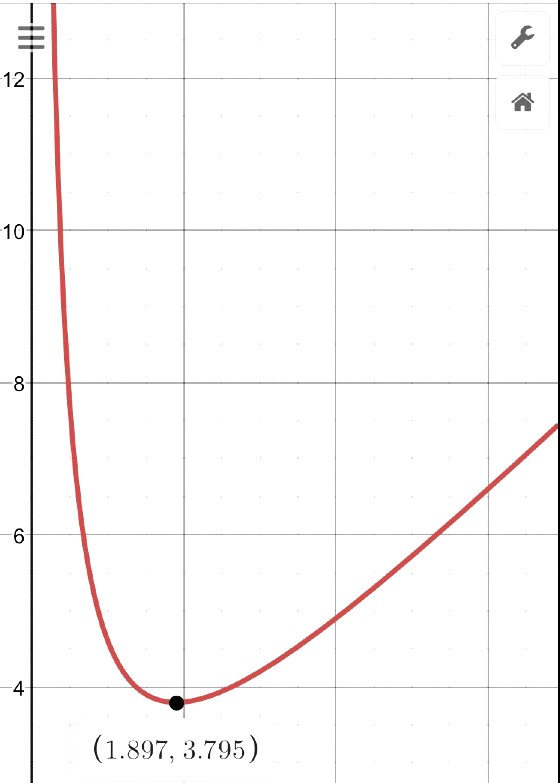
Since we are only interested in the value of x and not y, finding the x value for this maximum is no different from finding the z value of the minimum possible value of the curve in that region, likely arising from a minimum turning point.

6 - (x + 3.6/x) is a maximum means you want (x + 3.6/x) to be a minimum (as small as possible), since 6 is a constant.

This corresponds to the minimum value of y = x + 3.6/x

Find the minimum point on your graph, (which has the minimum value of y) first.
Then find the value of x that corresponds to it. Done.

You should be getting x ≈ 1.90

(Actual exact value is x = 1.897)

I presume that the lowest value of interest is the minimum point. I doubt the O Level examiners are so enthusiastic as to give a graph in which the boundary values, rather than minimum point, gives the minimum value of a curve.

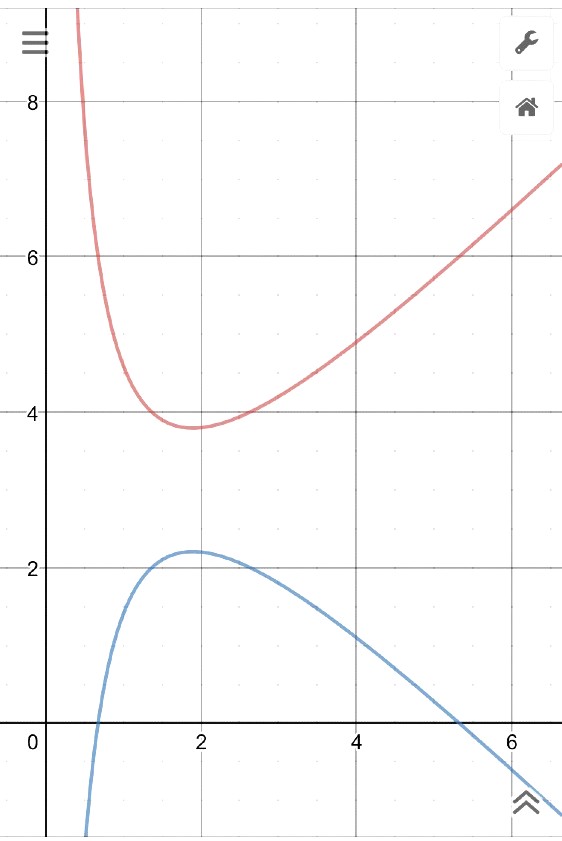
Sonia, I will plot the graph in a moment.

The question doesn't ask for any boundary for part d)

As in the boundaries 0.5 to 6.5 for the x values. Of course for this question, the minimum point also gives the minimum value of the curve.

I remember being tricked once, either during junior college or university, in the sense that the minimum point turned out to not give the minimum value of the curve. I can’t remember when and which question, but one such case is a y = ax3 + bx2 + cx + d graph, where the curve goes up first, then down, then up for a > 0. The minimum value comes from the leftmost boundary value of x given.

For some reason the term “minimum” in minimum point does get misleading at that level.

Minimum value within the boundary inclusive rather than minimum point (turning point) they meant.

But anyway the student will have to sketch the graph for this question so they wont be tricked (since the minimum value is easily spotted in the graph, whether turning point or not)

The more proper term for those minimum points (which aren't really the minimum) you described is 'local minimum/minima', which they don't really mention in syllabus. Neither do they talk about global maxima/minima in lower levels