Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | E Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Hi, can anybody help me with part(a)? Thank you so much!
If you observe carefully, this is a three dimensional object, but only two of the three dimensions change at different positions. These are the height and the length of the container, which is basically the triangular component of the container. The breadth, on the other hand, remains unchanged over time.
As a result, the container is not exactly a geometrically similar figure at different heights, but the triangle cross-section is similar at different heights.
As a result, only two of the dimensions change while the breadth remains unchanged, so the volume ratio at different height levels will be the same as the area ratio of the triangle or the square of the height ratio. Note that had the object really been geometrically similar at different heights, the volume ratio at different height levels will be the cube of the height ratio.
Since the height of the water level is 0.5 times the full height of the container, it follows that the area of the triangular surface of the water is 0.25 times the area of the entire triangular container (which is the square of 0.5, where the “square” reflects this two dimensional change; “cube” would have reflected a three dimensional change as one would see in geometrically similar objects).
Therefore, the time taken to fill up the water to that height is 0.25 times the time taken to fill up the entire container, so it takes 2 seconds (out of 8) to fill up the water to the halfway level.
Prisms can never be geometrically similar at different points within the objects since one of its dimensions remain unchanged.
See 1 Answer



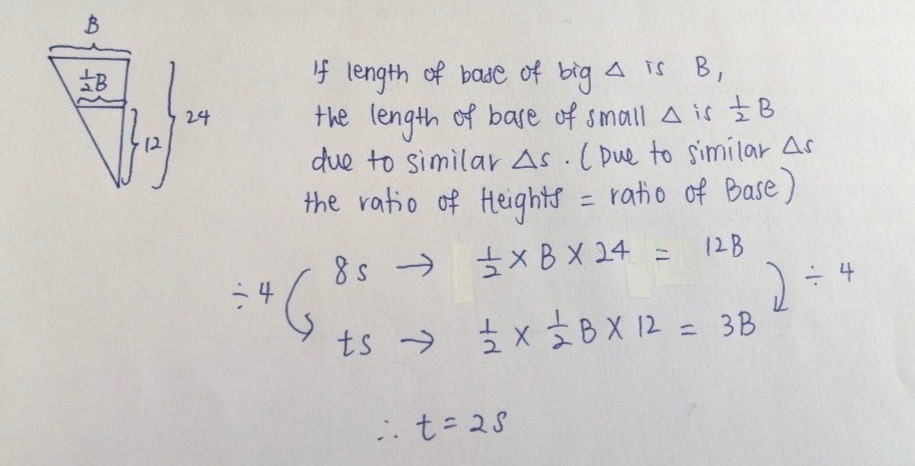


This is because the same volume of water fills up a “larger water cross sectional area”, hence slowing down the rate of increase of the height.