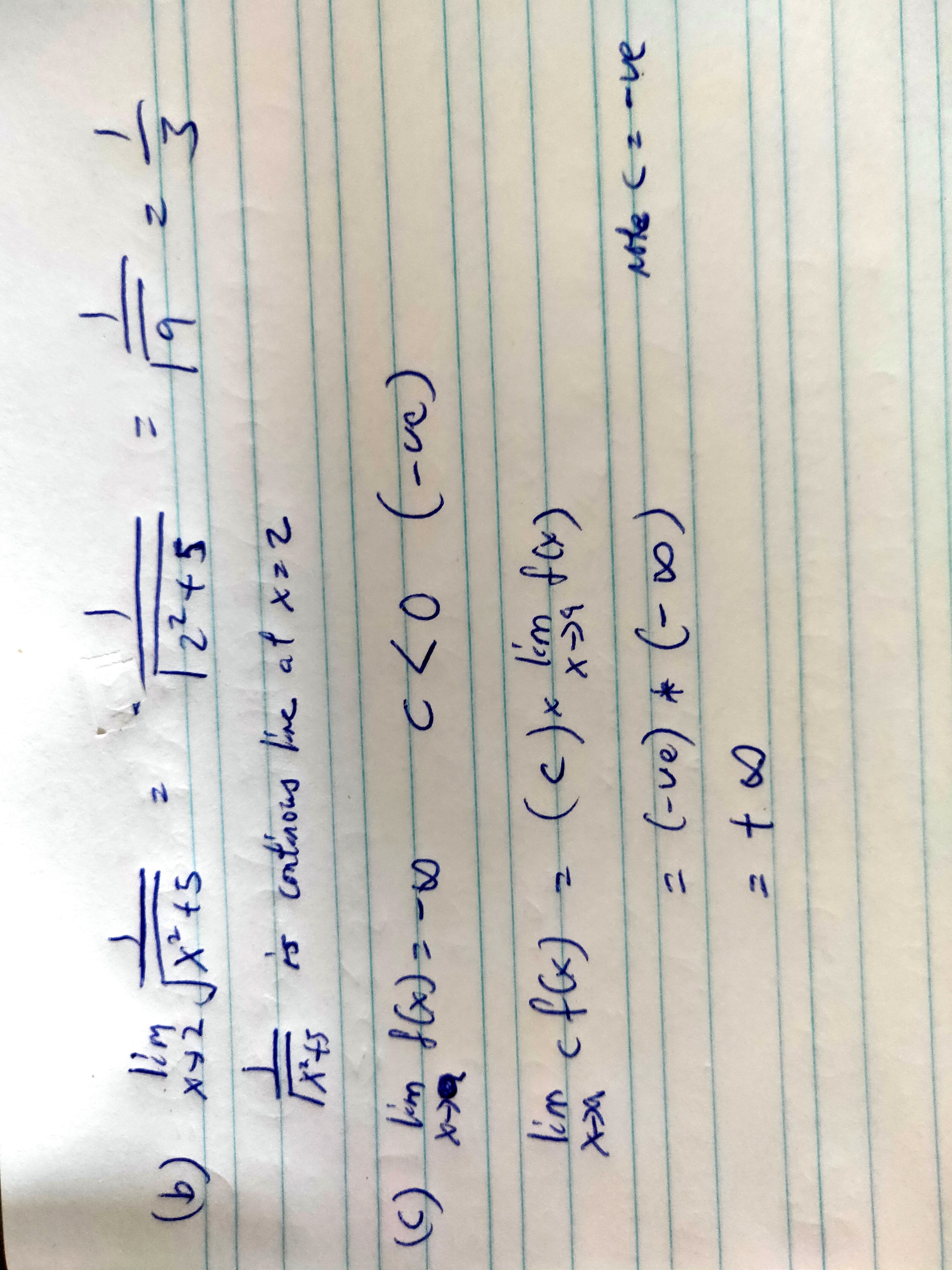https://www.math.ucdavis.edu/~kouba/CalcOneDIRECTORY/preclimsoldirectory/PrecLimSol.html#SOLUTION%2011 you might find this useful

b)

lim(x →a) f(x) = L

Given any real number ε > 0, there exists another real number δ > 0 such that if
0 < |x- a| < δ ⇒ | f(x) - L | < ε

lim (x→2) 1/√(x² + 5) = ⅓

So, 0 < |x-2| < δ ⇒ | 1 / √(x² + 5) - ⅓ | < ε

| 3 / 3√(x² + 5) - ⅓| < ε
| (3 - √(x² + 5) ) / 3√(x² + 5) | < ε

| (3 - √(x² + 5) ) / 3√(x² + 5) × (3 + √(x² + 5) ) / (3 + √(x² + 5) ) | < ε


| (3² - (x² + 5) ) / (9√(x² + 5) + 3(x² + 5) ) | < ε

| (4 - x²) / (9√(x² + 5) + 3(x² + 5) ) | < ε

| (2 - x)(2 + x) / (9√(x² + 5) + 3(x² + 5) ) | < ε

|2 - x| | (2 + x) / (9√(x² + 5) + 3(x² + 5) ) | < ε
|x - 2| |2 + x| | 1 / (9√(x² + 5) + 3(x² + 5) ) | < ε

Assume that δ ≤ 1
Then | x - 2 | < δ ≤ 1
-1 < x - 2 < 1
1 < x < 3

This means that:
3 < 2 + x < 5
So |2 + x| < 5

And,
14 < x² + 5 < 20

√14 < √(x² + 5) < √20

9√14 + 3(14) < 9√(x² + 5) + 3(x² + 5) < 9√20 + 3(20)

9√14 + 42 < 9√(x² + 5) + 3(x² + 5) < 9√20 + 60

1/(9√20 + 60) < 1/(9√(x² + 5) + 3(x² + 5))
< 1/(9√14 + 42)

So
| 1/9√(x² + 5) + 3(x² + 5)) | < 1 / (9√14 + 42)


Therefore,

|x - 2| |2 + x| |1/(9√(x² + 5) + 3(x² + 5))| < | x - 2 | (5) ( 1/(9√14 + 42) ) < ε

|x - 2| 5/(9√14 + 42) < ε

| x - 2 | < (9√14 + 42)/5 ε

So choose δ = min｛1, (9√14 + 42)/5 ε ｝


It follows that if 0 < |x-2| < δ ,

Then | 1 / √(x² + 5) - ⅓ | < ε