Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | A Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

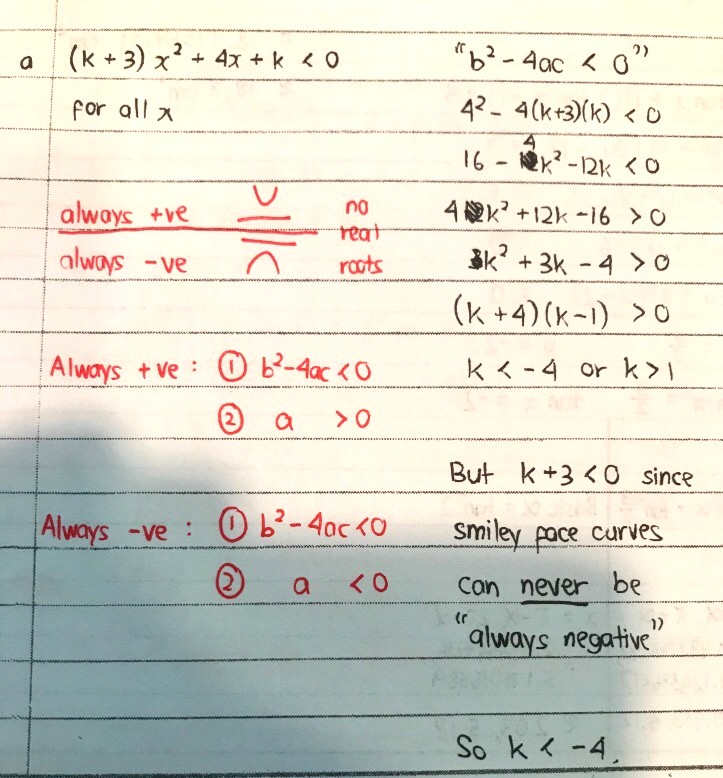
Good afternoon! I got k less than -4 or k more than 1 for part a, but the given anwer for the worksheet is k less than -4 only :/
Will write this up soon.
See 2 Answers
The distinguishing factor between always negative and always positive curves is the signage of the coefficient of x2. If a < 0, we get sad face graphs. If a > 0, we get smiley face graphs.
Note that smiley face graphs can never be “always negative”, since the curve will keep increasing indefinitely after the turning point. Similarly, sad face graphs can never be “always positive”, since the curve will keep decreasing indefinitely after the turning point.
1. b2 - 4ac < 0 (in all cases)
2. Signage of a; this will determine whether the curve is always positive or always negative
Let me know if you need more explanation and I will explain them to you again.
-9.17 < k < 9.17 ,
in order to be able to conclude that the smallest integer is -9. The marker can't tell from the expression √84 /-√84 alone