Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

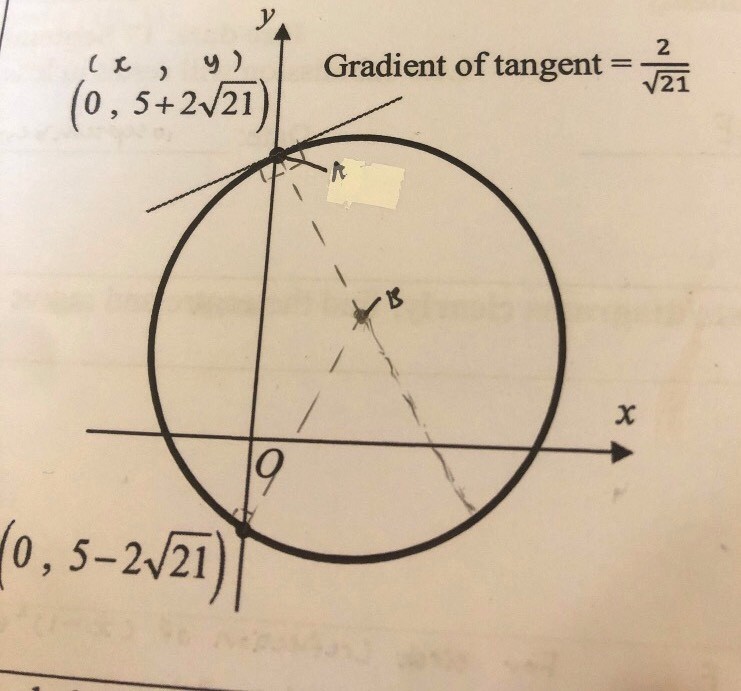
'Find the radius and centre'
Ok ive been staring at this qn for 2 days i still cant figure it out
y-coordinate of B is definitely 5.
We form one “normal to curve” equation at that tangent and then solve with y = 5 to find the x-coordinate of centre.
Radius is easy after thatz
See 1 Answer
Let coordinates of centre be (a,b)
Now radius is always the same from any point on the circle's circumference to the centre.
So length from each point to the centre is the same.
Use formula Length = √[(x2 - x1)² + (y2 - y1)²]
√[(0 - a)²+(5 + 2√21 - b)²] = √[(0 - a)²+(5 - 2√21 - b)²]
We can square both sides. Expression becomes
a² + (5 + 2√21 - b)² = a² + (5 - 2√21 - b)²
(5 + 2√21)² - 2b(5 + 2√21) + b² = (5 - 2√21)² - 2b(5 - 2√21) + b²
5² + 20√21 + 84 - 10b - 4b√21 = 5² - 20√21 + 84 - 10b + 4b√21
8b√21 = 40√21
b = 5
So the y coordinate is 5.