Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

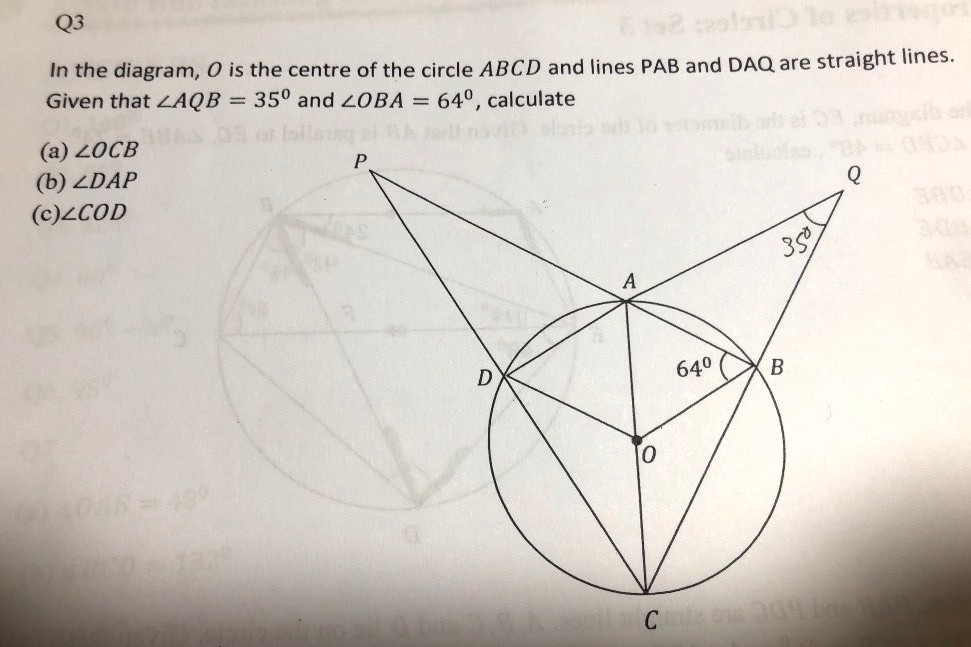
Question
secondary 3 | E Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

.
Angle ABC = 90° (angle in a semicircle)
Angle OBC = Angle ABC - Angle OBA
= 90° - 64° = 26° (complementary angles)
OB = OC
(both are radius of the same circle)
So △ OBC is isosceles.
Angle OCB = Angle OBC = 26°
(base angles of isosceles triangle are equal ,OB = OC)
Angle ABC = angle AQB + angle BAQ
(Exterior angle = sum of 2 interior opposite angles)
90° = 35° + Angle BAQ
So Angle BAQ = 90° - 35° = 55°
Since PAB and DAQ are straight lines,
then angle DAP = angle BAQ
(Vertically opposite angles)
= 55°
(Sum of angles on a straight line add up to 180°)
Angle CAB
= 180° - angle ABC - angle OCB
= 180° - 90° - 26°
= 64°
(Angle sum of triangle ABC)
Or
OA = OB (both are radius of same circle)
So triangle OAB is isosceles.
Angle OAB = angle OBA = 64°
(Base angles of isosceles triangle OAB, OA = OB)
Angle CAB = Angle OAB = 64°
(Common angles)
Then,
Angle DAC = 180° - Angle BAQ - angle CAB
= 180° - 55° - 64°
= 61°
(Sum of angles on a line DAQ)
Angle COD = 2 x angle DAC
(angle at centre = 2 x angle at circumference, relevant segment is CD)
2 x angle DAO (since DAO and DAC are common angles)
= 2 x 61°
= 122°
See 1 Answer