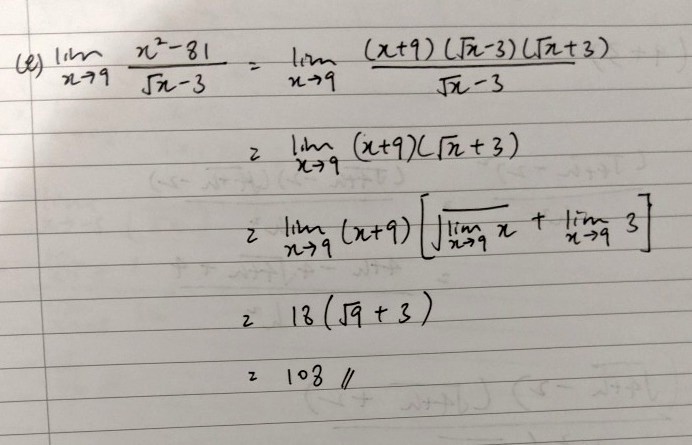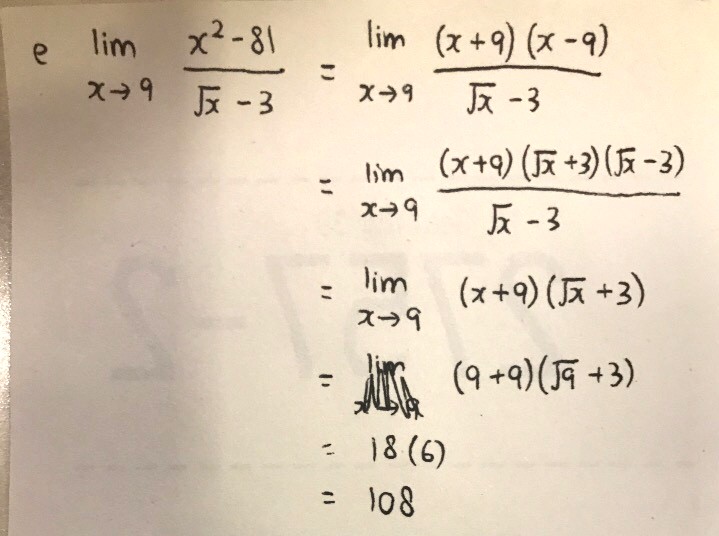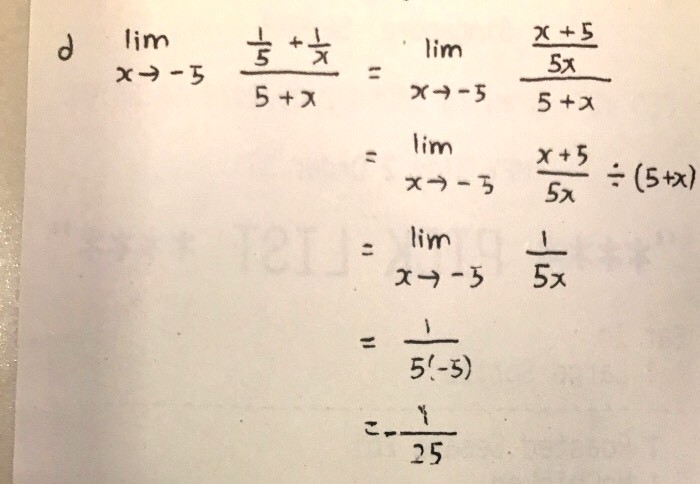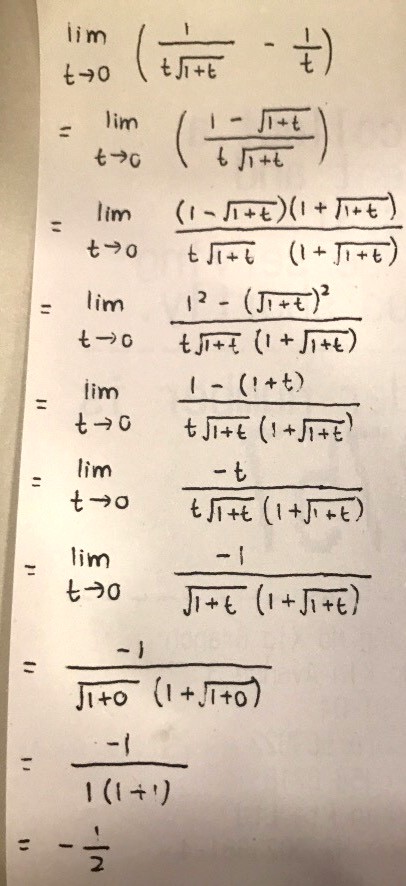Seems like you deleted the √x (1 + sin²(2π/x) ) question. Did you manage to solve it? I left a second comment on it which was my attempt on the question, not sure if you managed to see. If needed I'll type it out again

For b) the limit exists and is equal to ¼.

You'll have to use L'Hopital's rule here as both numerator and denominator end up becoming 0, and 0/0 is undefined.

https://math.oregonstate.edu/home/programs/undergrad/CalculusQuestStudyGuides/SandS/lHopital/zero_over_zero.html

So you'll get

lim (h→0) [√(4 + h) - 2)/h]

= lim (h→0) [ ( ½(4 + h)^(-½) ) / 1 ]

= lim (h→0) [ 1/(2√(4 + h)) ]

= 1/(2√4)

= 1/(2 x 2)
= ¼

I went to use another method for b

Yup, your method of doing the reverse of rationalising denominator works as well

@J, yes I saw it, thanks for helping for the prove ques!

Welcome. Eric's method is a good alternative to b) . Not many would think of reverse rationalisations

ok thanks! for part (e), does the limit exist?

Yes it does. It is 108. Let me write down the steps . Give me a while

Oops, never opened the pic and missed that there are three more questions

Part e is very similar. We factorise x2 - 81 continuously using a2 - b2 factorisation until we obtain the sqrt x minus 3.

lim (x →9) [ (x² - 81)/(√x - 3) ]

= lim (x →9) [(x² - 81)(√x + 3)/((√x - 3)(√x + 3))]


= lim (x →9) [(x + 9)(x - 9)(√x + 3)/(x - 9)]


= lim (x →9) [(x + 9)(√x + 3)]

= (9 + 9)(√9 + 3)

= 18 x 6

= 108

I got 108 as part (e) ans alr, thanks for all your help!

Just finished typing. Nice that you got 108 as well. Well done!

As for d), just multiply both numerator and denominator by x to solve.