Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

See 2 Answers
Your working seems fine to me! But maybe it can be clearer by adding an additional step to show the evaluation of the limit for the cube root, since you've shown it for the right hand side term as well.
eg. The left hand side
(1 + ³√(lim x² / lim(2x - 8) ) )
= (1 + ³√ (8²/ (2(8) - 8) )
= (1 + ³√8)
= (1 + 2)
eg. The left hand side
(1 + ³√(lim x² / lim(2x - 8) ) )
= (1 + ³√ (8²/ (2(8) - 8) )
= (1 + ³√8)
= (1 + 2)
ok thanks! :) I have another limit proving question, but idk how to present the ans using the squeeze theorem or precise definition of a limit, is it ok if you help me take a look?
I can only try! Kind of rusty at all these tbh





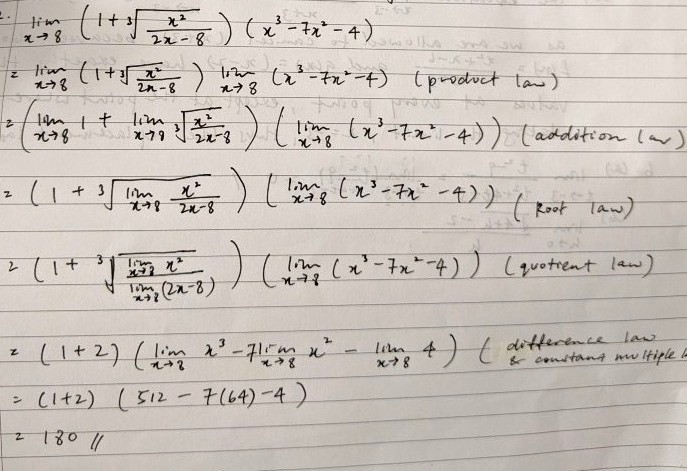


(1 + lim ( (x²/x²)/(2/x - 8/x²) )^⅓ ) ( lim(x³ - 7x² - 4) )
= (1 + (1/(2/8 - 8/8²))^⅓ ) (8³ - 7(8)² - 4)
= (1 + (1/⅛)^⅓ ) (512 - 448 - 4)
= (1 + 8^⅓)(60)
= (1 + 2)(60)
= 3 x 60
= 180