Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | E Maths
4 Answers Below
Anyone can contribute an answer, even non-tutors.

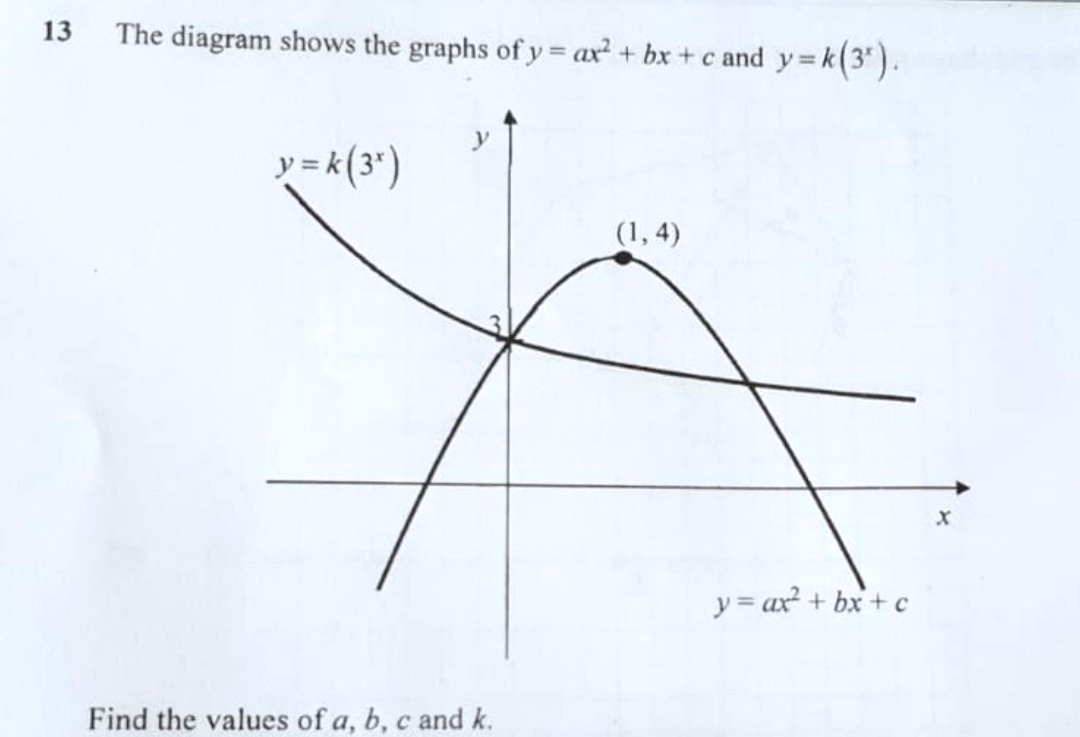
Sec 3 E maths qn. How to do? Please help thanks.
With Sec 4 A Maths techniques this question becomes straightforward.
I will write up the solutions later.
It should be y = k (3^-x).
y = 3 (3^-0.05x) models this equation better.
To fit the shape, 3^(-0.45x) + 2 looks better. Teachers really got to be careful in setting the graphs.
Also, If the assumption that (1,4) isn't minimum point this question probably is undoable
See 4 Answers
The downward-going graph should not have the equation y = k (3^x) because the graph of this equation is upsloping and fully above the y-axis for positive values of k and downsloping and fully below the y-axis for negative values of k.
A correct equation for such curves is y = k (3^-x).
c = 3 , k = 3, a + b = 1 (from Eric's above workings)
If the point (1,4) is taken as the maximum point, then it is tangent to the line y = 4. So it only meets that line at that one point.
We have y = 4 and y = ax² + bx + 3
4 = ax² + bx + 3
ax² + bx - 1 = 0
Since line meets the curve at only 1 point, there are real and equal roots. So discriminant (b² - 4ac) = 0
b² - 4a(-1) = 0
b² + 4a = 0 ①
Since a + b = 1, b = 1 - a ②
Sub ② into ①, (1 - a)² + 4a = 0
1 - 2a + a² + 4a = 0
a² + 2a + 1 = 0
(a + 1)² = 0
a + 1 = 0
a = -1
Then b = 1 - (-1) = 1 + 1 = 2