Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 2 | Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.
I need help with part b of this question thanks!
Date Posted: 4 years ago
Views: 234
See 1 Answer
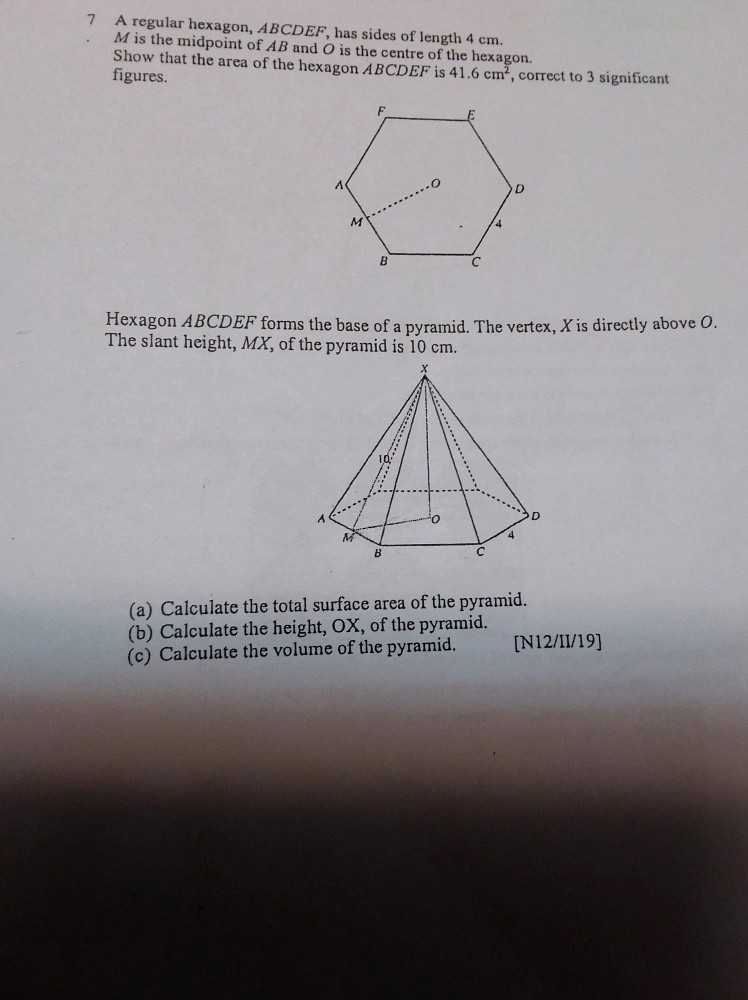
M is the midpoint of AB, so AM = MB.
MB = ½AB = ½ x 4cm = 2cm
If you managed to do the first part, you would know by now that the hexagon can be divided into 6 equilateral triangles. One of them is △OAB. Since AB is a side of the equilateral △ and AB = 4cm, OB = 4cm since all 3 sides of an equilateral triangle are equal in length.
△OAB is divided by line OM into two congruent right-angled triangles. △OMB is one of them.
Using Pythagoras' theorem, OM² + MB² = OB²
OM² = OB² - MB² = (4cm)² - (2cm)²
OM² = 16cm² - 4cm² = 12cm²
OM = √12 cm = √(4x3) cm = 2√3 cm
Now, △OMX is also a right-angled triangle.
So using Pythagoras' theorem again,
OM² + OX² = XM²
12cm² + OX² = (10cm)²
OX² = 100cm² - 12cm² = 88cm²
OX = √88 cm = √(4 x 22) cm = 2√22 cm
MB = ½AB = ½ x 4cm = 2cm
If you managed to do the first part, you would know by now that the hexagon can be divided into 6 equilateral triangles. One of them is △OAB. Since AB is a side of the equilateral △ and AB = 4cm, OB = 4cm since all 3 sides of an equilateral triangle are equal in length.
△OAB is divided by line OM into two congruent right-angled triangles. △OMB is one of them.
Using Pythagoras' theorem, OM² + MB² = OB²
OM² = OB² - MB² = (4cm)² - (2cm)²
OM² = 16cm² - 4cm² = 12cm²
OM = √12 cm = √(4x3) cm = 2√3 cm
Now, △OMX is also a right-angled triangle.
So using Pythagoras' theorem again,
OM² + OX² = XM²
12cm² + OX² = (10cm)²
OX² = 100cm² - 12cm² = 88cm²
OX = √88 cm = √(4 x 22) cm = 2√22 cm
To find OM , you can also use trigo.
∠MOB = 30° since OM bisects ∠AOB, which is 60°.
cos30° = OM/OB = OM/4cm
OM = 4(cos30°)cm = 4(√3 / 2)cm = 2√3cm
∠MOB = 30° since OM bisects ∠AOB, which is 60°.
cos30° = OM/OB = OM/4cm
OM = 4(cos30°)cm = 4(√3 / 2)cm = 2√3cm
360 Tutoring Program