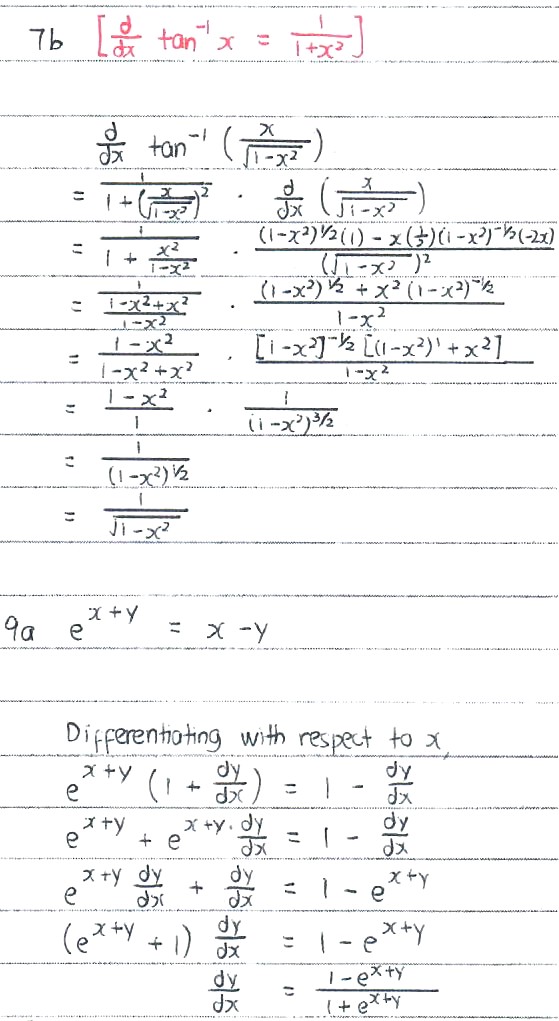7b)


d/dx ( tan‾¹ (x/√(1 - x²) )

= d/dx (tan‾¹ (x(1 - x²)-¹⁄²)

= 1/(1 + (x(1 - x²)-¹⁄²)² ) × (d/dx (x(1 - x²)-¹⁄²) )

= 1/(1 + x²(1 - x²)-¹ ) × ((1 - x²)-¹⁄² + x(-2x)(-½)(1 - x²)-³⁄² )

= 1/( (1-x²)-¹((1 - x²) + x²) ) × ( (1 - x²)-¹⁄² + x²(1 - x²)-³⁄² )

= 1/(1 - x²)-¹(1) × ( (1 - x²)-³/² ((1 - x²)+ x²) )

= (1 - x²) × (1-x²)-³⁄² (1)

= (1 - x²)¹-³⁄²

= (1 - x²)-¹⁄²

= 1/√(1 - x²)

9a)

e^(x + y) = x - y

Differentiate both sides with respect to x,


(1 + (1)dy/dx ) e^(x + y) = 1 - (1)dy/dx

e^(x + y) + e^(x + y) dy/dx = 1 - dy/dx


e^(x + y) dy/dx + dy/dx = 1 - e^(x + y)

dy/dx (e^(x + y) + 1) = 1 - e^(x + y)


dy/dx = (1 - e^(x + y) )/(1 + e^(x + y) )

Alternative to 7b)


Let y = tan‾¹ (x/√(1 - x²) )

Then tan y = (x/√(1 - x²) )


Differentiate both sides with respect to x,

sec²y (dy/dx) = ((1 - x²)-¹⁄² + x(-2x)(-½)(1 - x²)-³⁄² )


(1/cos y) dy/dx = ( (1 - x²)-¹⁄² + x²(1 - x²)-³⁄² )

dy/dx = (1 - x²)-³⁄² ((1 - x²)+ x²) ) cos y

dy/dx = (1-x²)-³⁄² (1)cos y



dy/dx = (1 - x²)-³⁄² (√(1- x²)/1)

= (1 - x²)-³⁄²+¹⁄²

= (1 - x²)-¹⁄²

= 1/√(1 - x²)




You may be wondering how did cos y get converted to √(1- x²)/1.

This is actually done by considering a right angled triangle with a designated angle y, with hypotenuse as 1, the opposite side as x, the adjacent as √(1 - x²)

(Based on tan y = (x/√(1 - x²) ) , so adj = x and opp = √(1 - x²)


Based on Pythagoras' Theorem we can say

adj² + opp² = hyp²

adj² = hyp² - opp² = 1² - x²

adj = √(1 - x²)

cos y = adj/hyp = √(1 - x²)/1



Since we are essentially differentiating
angle y when differentiating tan‾¹(x/√(1 - x²) ),

We can have a third alternative by restating it as differentiating sin‾¹(x/1) as it gives us the same angle y

sin‾¹(x/1) is just sin‾¹(x), which easily differentiates to 1/√(1 - x²) as you would have already learnt.

√(1 + xy) = 1/y

To make things easier, square both sides.

1 + xy = 1/y² = y‾²

Differentiate both sides wrt x,

y + x dy/dx = -2y‾³ dy/dx = -2/y³ dy/dx

x dy/dx + 2/y³ dy/dx = -y

(x + 2/y³)dy/dx = -y

dy/dx = -y/(x + 2/y³)

= -y⁴/(xy³ + 2)




Alternately,


√(1 + xy) = 1/y


Differentiate both sides wrt x,


½(1 + xy)‾¹⁄² (y + x dy/dx) = -1/y² dy/dx

y/(2√(1 + xy) ) + x/(2√(1 + xy) )dy/dx = -1/y² dy/dx


-y/(2√(1 + xy) ) = 1/y² dy/dx + x/(2√(1 + xy) )dy/dx


-y/(2√(1 + xy) ) = dy/dx (x/(2√(1 + xy) ) + 1/y²)

dy/dx = -y/(2√(1 + xy) ) × 1/(x/(2√(1 + xy) ) + 1/y²)


dy/dx = -y/( (2√(1 + xy) ) × 1/( (xy² + 2√(1 + xy) ) /(2y²√(1 + xy) ) )


dy/dx = -y/( (2√(1 + xy) ) × 2y²√(1 + xy) / ( xy² + 2√(1 + xy) )


= -y³/ (xy² + 2√(1 + xy) )

Don't worry about the different looking expressions for dy/dx, they are all interconvertible

Thank you !!!!

Welcome