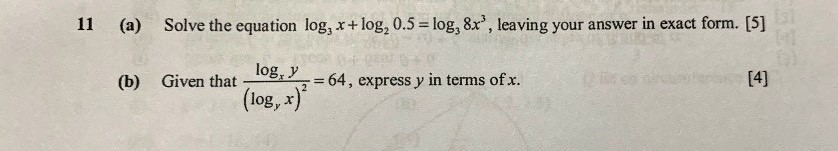Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

See 3 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
First one
Date Posted:
4 years ago
You can't divide 8x³ by x because that would be getting rid of a root.
log3(x) - 1 = log(8x³)
log3(x) - log3(3) = log(8x³)
log3(x/3) = log(8x³)
So
x/3 = 8x³
x = 24x³
24x³ - x = 0
x(24x² - 1) = 0
x(√24 x + 1)(√24 x - 1) = 0
(using property a² - b² = (a + b)(a - b) )
x = 0 or √24 x = 1 or √24 x = -1
(x = 0 is rejected as log3(x) is undefined for x ≤ 0 for real values of log3(x) )
x = 1/√24 or or x = -1/√24 (x = -1/√24 is rejected for the same reason as above)
x = √24/24
x = √(4 x 6) / 24
x = 2√6 / 24
x = √6 /12
log3(x) - 1 = log(8x³)
log3(x) - log3(3) = log(8x³)
log3(x/3) = log(8x³)
So
x/3 = 8x³
x = 24x³
24x³ - x = 0
x(24x² - 1) = 0
x(√24 x + 1)(√24 x - 1) = 0
(using property a² - b² = (a + b)(a - b) )
x = 0 or √24 x = 1 or √24 x = -1
(x = 0 is rejected as log3(x) is undefined for x ≤ 0 for real values of log3(x) )
x = 1/√24 or or x = -1/√24 (x = -1/√24 is rejected for the same reason as above)
x = √24/24
x = √(4 x 6) / 24
x = 2√6 / 24
x = √6 /12
Right, good point.
But I presume that here is ok because the missing roots are always zero roots and log(any) 0 is undefined.
But I presume that here is ok because the missing roots are always zero roots and log(any) 0 is undefined.
Loss of marks will ensue due to elimination of a root too early
i.e all roots should be found first, then rejection is done if required
i.e all roots should be found first, then rejection is done if required
Hmmm...interesting point
It's the same for the 24x² = 1. We could have just skipped the negative root and write x = 1/√24, knowing that log3(-ve) is undefined.
But that would result in deduction of marks. Because x = -1/√24 are also valid roots of the equation 24x² - 1 = 0. Likewise for x = 0 for the equation 24x³ - x = 0.
it's because the original equation had the log3( ), so in the context of the question , we reject them.
There is a need to find the negative root and show why the negative root is rejected. Since the zero root carries equal weight as the other roots, it must also be shown that it exists but is rejected.
But that would result in deduction of marks. Because x = -1/√24 are also valid roots of the equation 24x² - 1 = 0. Likewise for x = 0 for the equation 24x³ - x = 0.
it's because the original equation had the log3( ), so in the context of the question , we reject them.
There is a need to find the negative root and show why the negative root is rejected. Since the zero root carries equal weight as the other roots, it must also be shown that it exists but is rejected.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Second one
Date Posted:
4 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Updated
Date Posted:
4 years ago