Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Need help with question 13. It requires you to somehow find the value without applying any integration rules. Topic is area of a region. Source: Additional Maths 360. All help appreciated!
1 represents the length of the hypotenuse of a right angled triangle.
x represents the length of 1 side of it, and it's part of the x axis.
y represents the length of the third side of the triangle, and is parallel to the y axis.
Using Pythagoras theorem,
x² + y² = 1²
y² = 1 - x²
y = ± √(1 - x²)
We only consider the positive part as the negative part is another semicircle , a reflection of this semicircle along the x axis.
So the hypotenuse length is fixed at 1 but the x and y coordinates are variable.
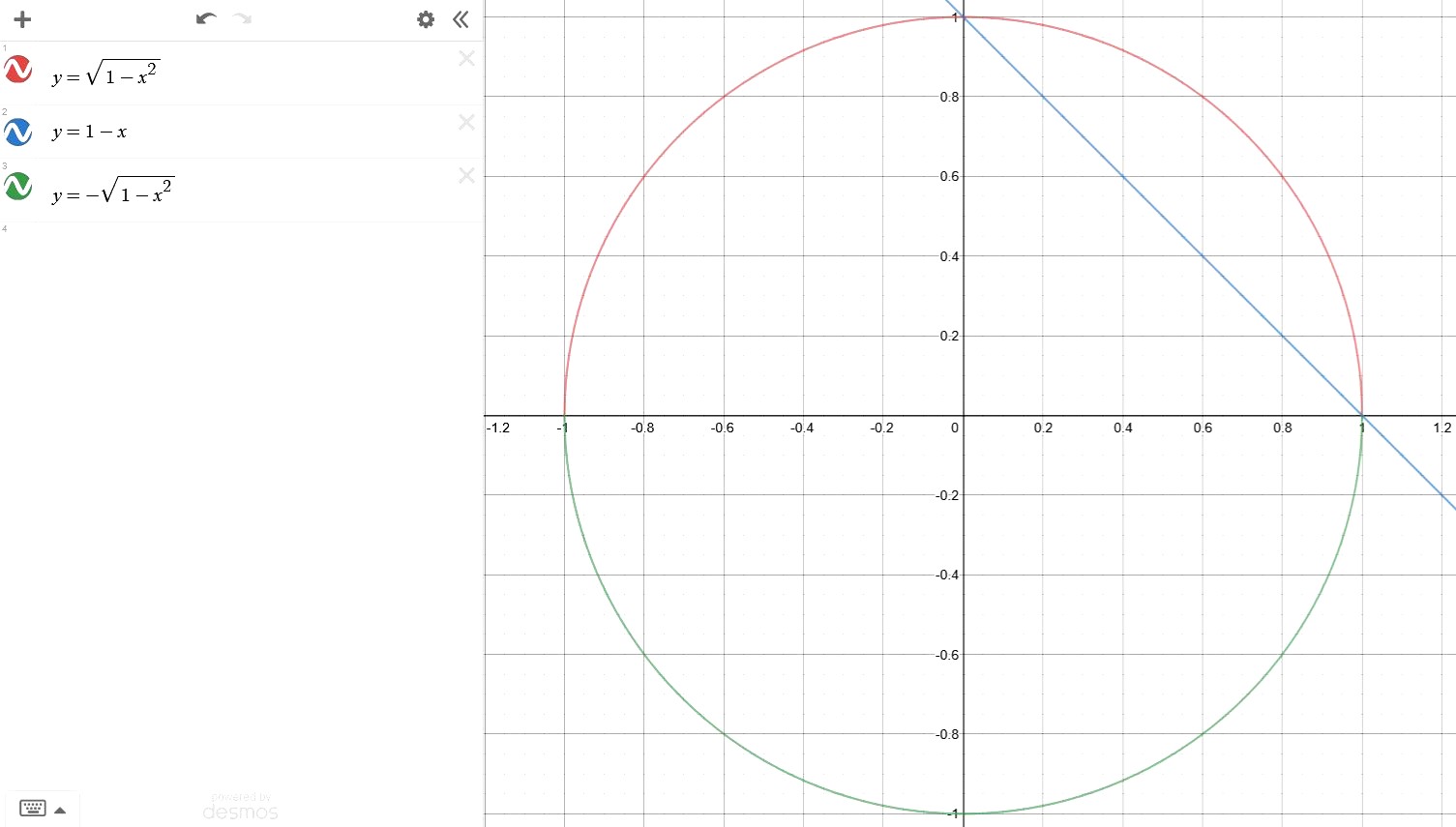
You'll see that all the coordinates on the graph form a semicircle with radius of 1 unit.
From x = 0 to x = 1, it's a quarter circle.
Area of quarter circle = ¼π(1units)²
= ¼π units²
The line y = 1 - x forms a right angled isosceles triangle with the x and y axis, with x intercept 1 and y intercept 1.
Area of this triangle is = ½ x 1 x 1 = ½ units²
Required area
= Area of quarter circle - area of triangle
= ¼π units² - ½ units²
= ¼ (π - 2) units²
You are essentially finding a small half-leaf/segment
The two semicircles form a circle with centre (0,0) and radius 1
From x² + y² = 1²
(x - 0)² + (y - 0)² = 1²
The straight line will form a right angled triangle with the x-axis.
From there we just calculate the integral by the sum/difference of areas.
y = √(1 - x²) would need some inference from the Pythagoras' theorem or circle equation. They are linked.
Technically not the same as circle, but derived from it.
Anyway it's a H.O.T corner question so it's more of a higher order thinking question that goes beyond the mere usual applying of integration/expand the student's horizons/connecting the dots.
It won't come out in national exams
See 1 Answer
I have included the graph of the curve (in red), the straight line (in blue) and an additional graph below the x-axis (in green) to illustrate J's point that the equation of the curve is actually that of a (semi) circle with the origin (0, 0) as its centre and radius 1 unit.
To describe in words, the integral gives the area of the region bounded by the curve y = sqrt (1 - x^2) and the line y = 1 - x.
As we well know it, this area is simply the area of the quarter circle (quadrant) with radius 1 unit minus the area of the triangle.
Value of integral
= Area of quadrant - Area of triangle
= 1/4 x Pi x 1 x 1 - 1/2 x 1 x 1
= (Pi/4 - 1/2) units^2