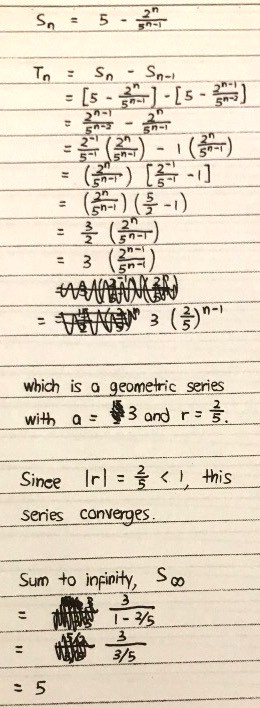5 - 2ⁿ/5ⁿ‾¹

= 5 - 2ⁿ/(5ⁿ(5‾¹))

= 5 - 5(2ⁿ)/5ⁿ

= 5 - 5(2/5)ⁿ

= 5(1 - (2/5)ⁿ)

= 5(1 - 2/5)(1 - (2/5)ⁿ)/(1 - 2/5)

= 3(1 - (2/5)ⁿ)/(1 - 2/5)

The sum of the first n terms of this series can be rewritten as the expression for the the sum of the first n terms of a geometric series

Sn = a(1 - rⁿ)/(1 - r)

having the first term, a = 3
and common ratio, r = 2/5

Therefore the series is a geometric series.



ii)

Since |r| = |2/5| = 2/5 < 1,

the series converges as each subsequent term is smaller than the previous (technically a proper fraction of the previous term), i.e the terms are getting smaller as n increases.

Sum to infinity, S∞

= a/(1 - r)

= 3/(1 - 2/5)

= 3/(3/5)

= 3 x 5/3

= 5

Interesting approach. I have forgotten most of my JC stuff already, so I simply used Tn = Sn - S(n - 1).

Thank you for the explanation

Welcome, Janet.

Funny thing is, i remember the sum formula but the basic Tn = Sn - S(n-1) didn't cross my mind at all

Janet, to add in my workings, we must make sure that Tn must equal to...

...the starting number A times R raised to the power of (n - 1).

It’s not power n, because the starting term is A, which is the same as A times R^(1 - 1) where n = 1 represents the first term. I made this error the first time.