a)

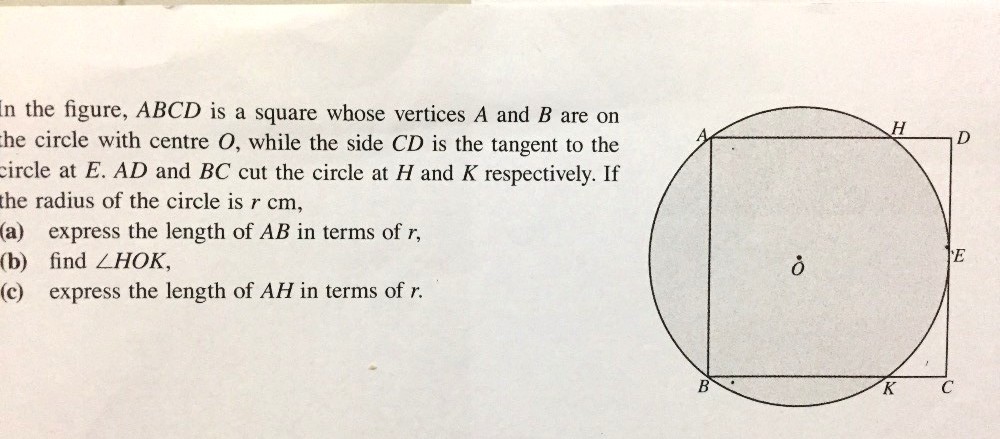
Draw the line KH and OE.

OE is perpendicular to tangent CD
(tangent is perpendicular to radius)

Since OE passes through the centre,
Chord KH is perpendicular to OE.

(the perpendicular bisector of a chord passes through the centre)

Since OE is perpendicular to both CD and KH, this implies KH // CD.

Since K and H lie in opposite sides of the square and KH // CD, KH is equal to a side of the square and KH = CD = AB

So AHKB is a rectangle.

Let perpendicular distance from circumference to chord AH be a cm.

AH = BK so perpendicular distance from circumference to chord BK also = a cm.

(equal chords are equidistant from the centre. Which in turn means the perpendicular distance to the circumference is also the same since it equals (radius - distance from centre) )

Distance between the two chords
= Diameter - 2 perpendicular distance from circumference
= 2r - 2a
= Length of a side of the square.

AB is a side of the square so AB = 2r - 2a

HKCD is also a rectangle.

KC = perpendicular distance from E to KH since KC is parallel to OE.

Now,
BK = BC - KC
BK = AB - KC (since BC = AB)
BK = 2r - 2a - KC ①

Now AB and KH are equal chords of the circle. So perpendicular distance from circumference to AB also = KC

Distance between the two chords AB and KH
= Diameter - 2 perpendicular distance from circumference
= diameter - 2KC
= 2r - 2KC

Distance between two chords AB and KH
is just the width of the rectangle so it = BK.

So BK = 2r - 2KC ②

Since ① = ②,

2r - 2a - KC = 2r - 2KC
KC = 2a

So BK = 2r - 2(2a) = 2r - 4a

ABK is a right angled triangle, with AK as the hypotenuse.
AK is a diameter of the circle so AK = 2r.


Using Pythagoras Theorem,

AB² + BK² = AK²

(2r - 2a)² + (2r - 4a)² = (2r)²

4r² - 8ar + 4a² + 4r² - 16ar + 16a² = 4r²

4r² - 24ar + 20a² = 0
r² - 6ar + 5a² = 0
(r - 5a)(r - a) = 0
r = 5a or r = a

(r = a is rejected, because a < r.
if r = a,
AB = 2a - 2a = 0
and BK = 2a - 4a = -2a, which is negative. lengths cannot be 0 or negative)

So r = 5a
a = r/5

AB = 2r - 2a
= 2r - 2(r/5)
= 8r/5

b)


KH = AB = 8r/5

Let the foot of the perpendicular from O to HK be F.

Since OE bisects KH, KF = ½KH
= ½(8r/5)
= 4r/5

Triangle HOK is divided by OE into 2 congruent right angled triangles , KOF and HOF. OE bisects angle HOK.

KO is just a radius of the circle so KO = r

Using trigo,

sin ∠KOF = opp/hyp
= KF/KO
= (4r/5)/r
= 4/5

∠KOF = sin‾¹(4/5)


Since OE bisecs ∠HOK ,
∠ HOK = 2 ∠KOF
= 2sin‾¹(4/5)
≈ 106.2602048°
= 106.3° (1 d.p)



c)

AH = BK

= 2r - 4a

= 2r - 4r/5

= 6r/5

TQ very much. It’s rather complicated

Welcome. This question is slightly more advanced for sec 2.

For a) you may skip the proving part (probably can assume some things without proving) .

The most important is to show the two equations of BK and equate them

TQ teacher for your advice