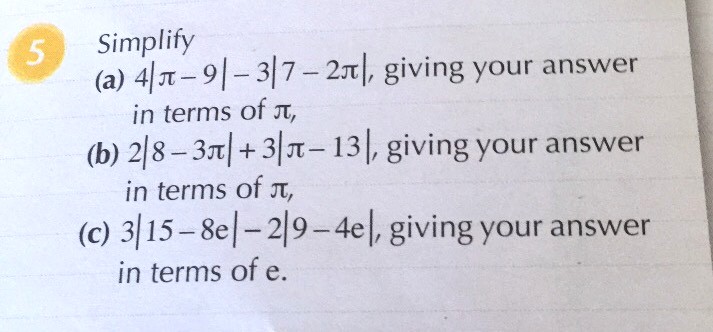Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 4 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Pls help with at least one question. Preparing for o levels. Pls help. Thank you!
4|π - 9| - 3|7 - 2π|
Since this question is about absolute value, we check the value to see if it's negative or positive first.
Now we know π is about 3.142. so π - 9 is definitely negative.
So we need to swop the sides of π and 9 to make it positive when calculated since absolute value is always positive.
2π would be about 6.284. it's definitely smaller than 7. So 7 - 2π is positive. We can leave it as it is.
Therefore,
4|π - 9| - 3|7 - 2π|
= 4 (9 - π) - 3(7 - 2π)
= 36 - 4π - 21 + 6π
= 15 + 2π
When unsure of negative or positive, use calculator to check. Then decide to swap or not, based on the result.
After doing the other 2 questions, you can type your answers here and I can check them for you to see if you got it right, if you like.
See 1 Answer
Suppose you have |8 - 3|. Clearly the term inside the modulus brackets is positive (at 5), which remain unaffected as the modulus brackets are removed. Hence, |8 - 3| is the same as simply (8 - 3).
However, suppose you have |3 - 8|. Clearly the term inside the modulus brackets is negative (at -5), which will become positive (5) as the modulus brackets are removed, as though we are actually writing 8 - 3. Hence, we will need to swap the positions and write |3 - 8| as (8 - 3).
Here, it’s a similar idea, except that your final answers are to be left in terms of pi or e, so we are not allowed to present our answers in irrational decimal form. What we can do, however, is to use our calculator as a guide to see whether there value of the contents of the modulus brackets is positive or negative, so that we would know whether to swap the positions or not after removing the modulus brackets.
Let me know if you need more explanation and I will do my best to explain them to you again!