Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 1 | H1 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Please help thanku :)
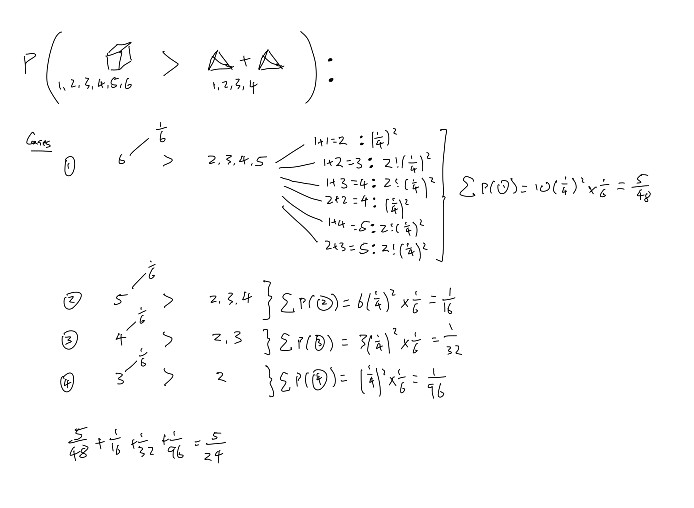
1,2,3,4,5,6
Since the highest score for 6 sided die is 6, and we're finding the outcomes for the total of two 4 sided dice being smaller than the score of that 6 sided die,
Possibilities that we only need to consider for the two 4 sided dice:
1,1 (total 2)
1,2 or 2,1 (total 3)
1,3 or 3,1 (total 4)
2,2 (total 4)
1,4 or 4,1 (total 5)
2,3 or 3,2 (total 5)
So we can have the following outcomes :
(6 side score vs total score of two 4 side )
①
3 vs 2 (1,1)
4 vs 2 (1,1)
5 vs 2(1,1)
6 vs 2(1,1)
②
4 vs 3 (2,1 or 1,2)
5 vs 3 (2,1 or 1,2)
6 vs 3 (2,1 or 1,2)
③
5 vs 4 (2,2)
6 vs 4(2,2)
④
5 vs 4(1,3 or 3,1)
6 vs 4 (1,3 or 3,1)
⑤
6 vs 5 (1,4 or 4,1)
6 vs 5 (2,3 or 3,2)
So there are 13 outcomes we can consider. There can be 2 or 1 possible ways for each outcome depending on the permutation of the 4 sided dice.
Whether we consider the two 4 sided dice to be different or identical/indistinguishable, there will be 96 possibilities for the throws regardless. But there will only be 60 distinguishable outcomes if your two dice are identical and indistinguishable. (refer to other comment)
(6 possibilities for the 6 sided die x 4 possibilities for the 1st 4 sided die x 4 possibilities for the 2nd 4 sided die = 96)
So for the 13 outcomes,
Total possibilities :
①
3 vs 2 (1,1)
4 vs 2 (1,1)
5 vs 2(1,1)
6 vs 2(1,1)
4 different cases x 1 way each = 4
②
4 vs 3 (2,1 or 1,2)
5 vs 3 (2,1 or 1,2)
6 vs 3 (2,1 or 1,2)
3 different cases x 2 ways each = 6
③
5 vs 4 (2,2)
6 vs 4(2,2)
2 different cases x 1 way each = 2
④
5 vs 4(1,3 or 3,1)
6 vs 4 (1,3 or 3,1)
2 different cases x 2 ways each = 4
⑤
6 vs 5 (1,4 or 4,1)
6 vs 5 (2,3 or 3,2)
2 different cases x 2 ways each = 4
Total = 4 + 6 + 2 + 4 + 4 = 20 possibilities
Probability = 20/96
= 5/24
See 1 Answer
If you encounter a similar question that asks for the number of distinguishable outcomes instead
The two 4 sided dice are probably considered identical so some of the permutations have to be removed since it would be considered as double counting.
If the 2 dice are identical, then order doesn't matter as they are thrown at the same time and one doesn't take note of which is which.
For the 13 outcomes,
Total possibilities :
①
3 vs 2 (1,1)
4 vs 2 (1,1)
5 vs 2(1,1)
6 vs 2(1,1)
4 different cases x 1 way each = 4
②
4 vs 3 (2 + 1)
5 vs 3 (2 + 1)
6 vs 3 (2 + 1)
3 different cases x 1 way each = 3
③
5 vs 4 (2,2)
6 vs 4(2,2)
2 different cases x 1 way each = 2
④
5 vs 4 (1 + 3)
6 vs 4 (1 + 3)
2 different cases x 1 way each = 2
⑤
6 vs 5 (1 + 4)
6 vs 5 (2 + 3)
2 different cases x 1 way each = 2
Total cases to be considered
= 4+3+2+2+2
= 13
So number of distinguishable outcomes where the 6 side die score is higher than the two 4 sided dice' combined score
= 13
Cases for 4 sided dice that would be double counted:
1,2 and 2,1
1,3 and 3,1
1,4 and 4,1
2,3 and 3,4
2,4 and 4,2
3,4 and 4,3
For each of these there are 6 choices for the 6 sided die score.
6 choices x 6 cases per choice that are double counted
= 36 cases
Actual number of distinguishable outcomes
= 6 x 4 x 4 - 36
= 96 - 36
= 60
1. rolling and getting 1 in the first roll and then rolling and getting 3 in the subsequent roll
is distinct from
2. rolling and getting 3 in the first roll and then rolling and getting 1 in the subsequent roll.
you have to add these two probabilities together even though their sum is the same, but precisely because u can have 2 cases with the same probabilities resulting in the same numerical sum, your chances are doubled.
So since the two dice are identical, they won't be distinguishable in a typical roll.
Your working would be for the case where the two 4 sided dice were rolled separately.
When i flip two coins, both being completely identical, the table of values would be:
HH TH HT TT
The probability of getting a (heads tgt with tails) is 1/4 + 1/4 = 1/2
By your logic, it would turn out like this
Cases of HT = 1
Total cases (Minus the double counting of HT and TH) = 4 - 1 = 3
The probability of getting a (heads tgt with tails) then will be 1/3.
Which isn’t very correct
2 heads
2 tails
1 head and 1 tail (not distinguishable since coins are identical)
When you flip the coins , you won't be keeping track of which is which.
By considering HT and TH, you are already assigning a different identity to each coin or already keeping track of which coin is which when flipping.
This would be the same as flipping the two coins separately, and considering both HT and TH
probability of getting a heads and tails,
the answer you get is 0.5
In my second working (above) I was actually finding the number of distinguishable outcomes and the percentage of those distinguishable outcomes where the score of the 6 sided die was higher than the combined score of two sided die.
The question asked for probability so even if the dice were identical and indistinguishable, both the actual outcomes whereby dice 1 and 2 roll x,y and y,x respectively have to be considered as they are part of the total probability. Similar to the number of distinguishable outcomes if one die was green and the other yellow. I'll edit the above answer.
Yeon Jae, I've typed an alternative working earlier that considers the approach in finding the different cases is in the main comments section. Feel free to check it out.