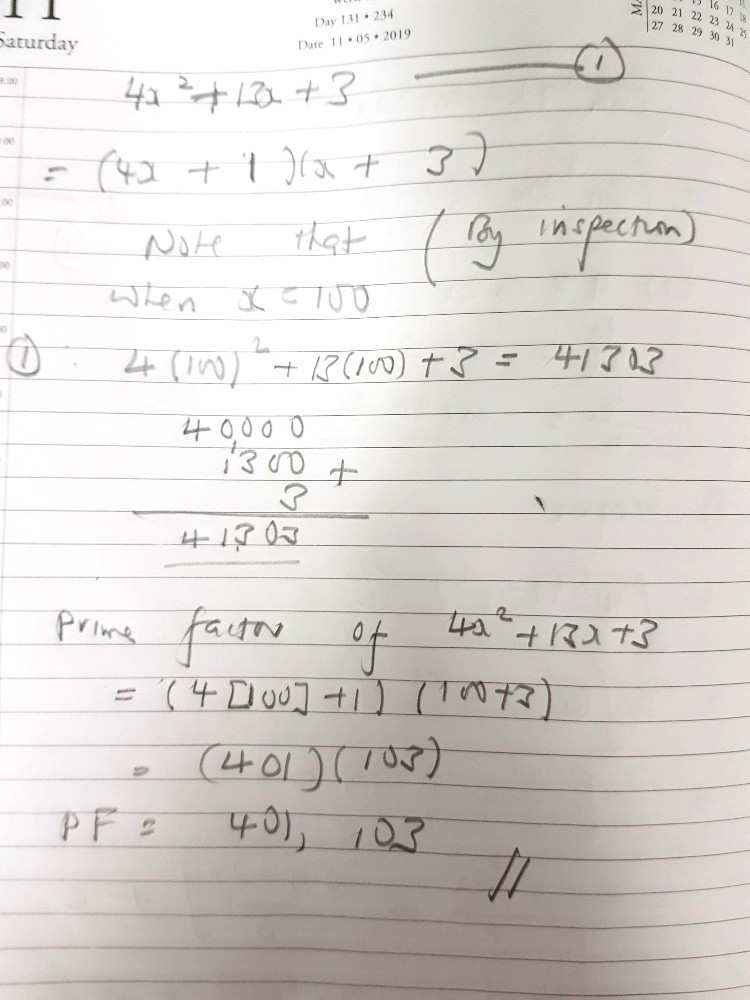4x² + 13x + 3

= (4x + 1)(x + 3)

You can do this by the usual method you're taught.


Now notice that the numbers in 41303 look very similar to the coefficients of the quadratic equation above.

The idea here is to rewrite the number as a sum of 3 numbers, then factor out the corresponding coefficients of the quadratic equation for each number.

41303 = 40000 + 1300 + 3

= 4 x 100 x 100 + 13 x 100 + 3

= 4 (100)² + 13(100) + 3


If you let 41303 = 4x² + 13x + 3,

Then 4(100)² + 13(100) + 3 = 4x² + 13x + 3

Compare the two sides and you'll realise x = 100


Since (4x + 1)(x + 3) cannot factorised further, they must be the prime factors of 4x² + 13x + 3. Recall that the prime factor can only be divided by 1 or itself.

Since x = 100, the prime factors of 41303 would be

4(100) + 1 = 401

And

100 + 3 = 103.

Though it’s true that (4x + 1) (x + 3) is the fully factorised form of 4x2 + 13x + 3, I cannot vouch for sure that this method will get us the prime numbers all the time.

In this instance, yes, 401 and 103 are indeed prime numbers. I have compared this against the list of prime numbers.

However, this only works for some values of x. For example, x = 1000 fails because 1003 is not a prime number (1003 = 17 x 59). In other words, if x = 1000, then 4013003 = 4001 x 1003 is not the simplest we can go.

So I am currently wondering, these types of questions (which I have answered several times already by now) rely on the assumption that the numbers obtained from such factorisations are prime.

Students tend to assume that the two numbers obtained are prime without bothering to check whether these numbers are actually prime or not.

Thanks for the explanation, it really helped

There isn't really a need to check here, as the question has been designed such that the two factors will be prime for this value of x. (Or in other words, the number is a product of two primes) If not they would not mention 'hence, use your result ... ...'.

The setters typically would not be so evil/tricky to put the factors as non prime, and expect the student do an extra step of further factorisation. So far in my experience there hasn't been any question like this.

This question is likely to have been designed by first coming up with (4x + 1)(x + 3), then using a suitable value of x to get prime factors, before expanding to get 4x² + 13x + 3.

Of course if the student wants to be absolutely sure he/she can always check..