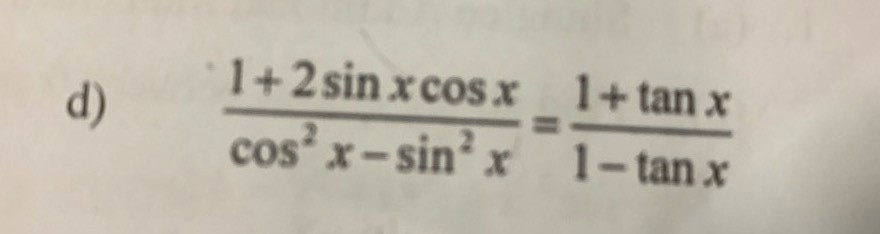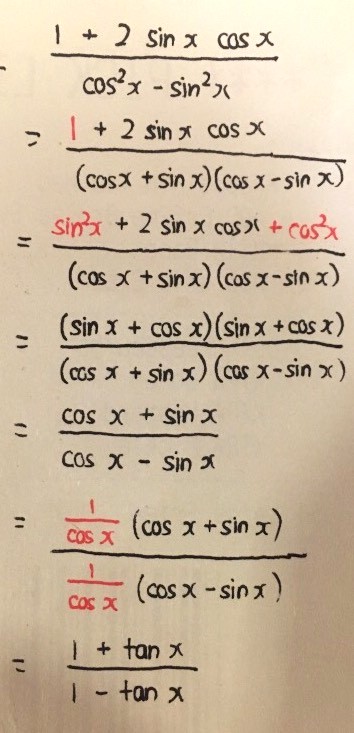Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

how to prove the following identity pls help thank you
(Property applied here is a² - b² = (a + b)(a - b) )
② Change 1 + 2sinxcosx to sin²x + cos²x + 2sinxcosx, (use property cos²x + sin²x = 1)
which = (sinx + cosx)²
(Property used here is (a + b)² = a² + 2ab + b²)
③ Then cancel out (cosx + sinx) on both the numerator and denominator. This leaves (cosx + sinx)/(cosx - sinx)
④ Divide both numerator and numerator by cosx.
This leaves (1 + sinx/cosx)/(1 - sinx/cosx)
, which equals (1 + tanx)/(1 - tanx)
(1 + 2sinxcosx)/(cos²x - sin²x)
= (sin²x + cos²x + 2sinxcosx)/(cos²x - sin²x)
= (sin²x/cos²x + cos²x/cos²x + 2sinxcosx/cos²x)/(cos²x/cos²x - sin²x/cos²x)
= (tan²x + 2sinx/cosx + 1)/(1 - tan²x)
= (tan²x + 2 tanx + 1)/( (1 + tanx)(1 - tanx) )
= (tanx + 1)² / ( (1 + tanx)(1 - tanx) )
= (tanx + 1)/(1 - tanx)
See 1 Answer