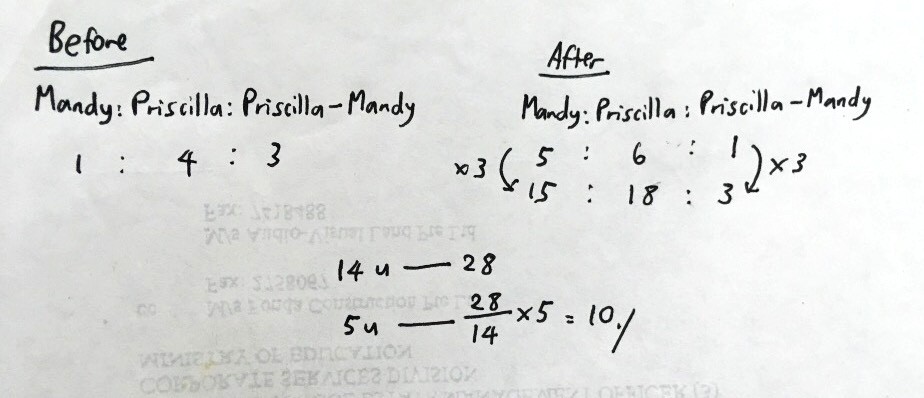Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
primary 6 | Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

How to solve? Stuck.
before
M: u
P: 4u
after
M: u+28
P: 4u+28
u+28 : 4u+28 = 5 : 6
6(u+28) = 5(4u+28)
u = 2
total stickers in pack = 10
It's as good as saying Priscilla had 6 units, and Mandy had 5 units. So Priscilla has 1 unit more than Mandy. And this 1 unit is 1/5 of Mandy's 5 units.
Alternative method :
Notice that the difference in their number of stickers before and after obtaining 28 stickers each, is the same. This is so as they bought the same number of stickers.
Before:
Ratio of Mandy to Priscilla = 1 : 4
Difference = 4 units - 1 unit = 3 units
After :
Ratio of Mandy to Priscilla = 5 : 6
Difference = 6 units - 5 units = 1 unit
Since the difference is the same before and after, the number of units should be the same. So we make them the same.
Multiply by 3,
After :
Ratio of Mandy to Priscilla = 5 : 6 = 15 : 18
Difference = 1 unit x 3 = 3 units
So if we compare this with the ratio for 'before',
15 - 1 = 14
18 - 4 = 14
There is an increase of 14 units for each girl's number of stickers.
So 14 units = 28 stickers
1 unit = 28 stickers ÷ 14 = 2 stickers
Number of units at first = 4 + 1 = 5
So number of stickers in the packet
= 2 stickers x 5
= 10 stickers
See 1 Answer