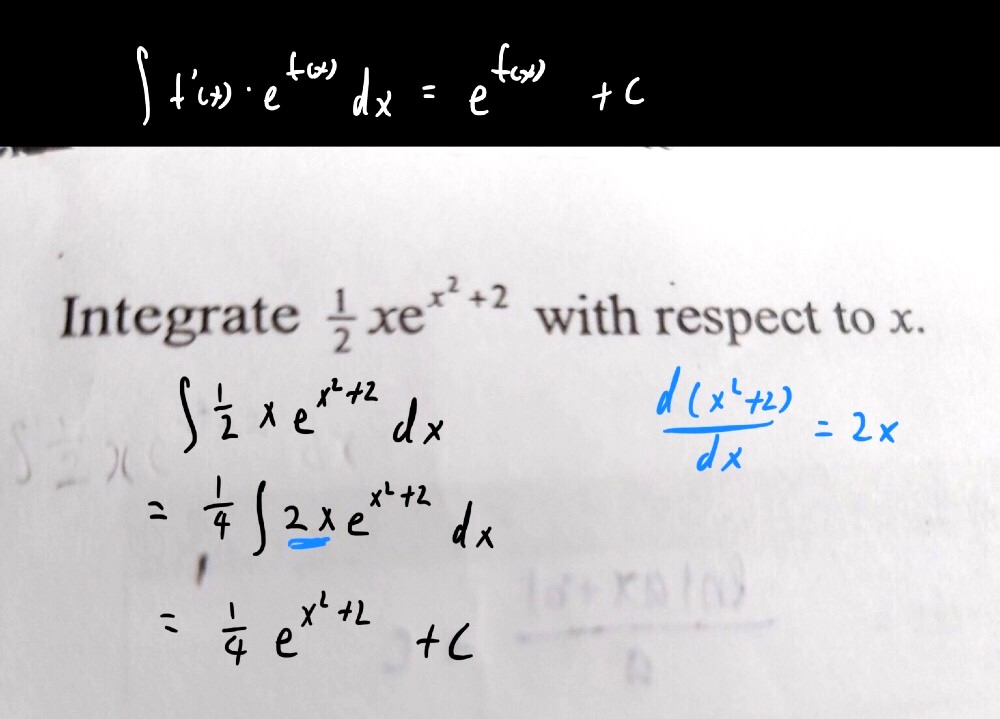Realise that when you differentiate e^(x² + 2), you get 2xe^(x² + 2)

(Differentiating the x² + 2 gives you 2x , which you bring down.)

So you can just rewrite ½xe^(x² + 2) as

¼( 2xe^(x² + 2) )

The whole expression within the outer brackets is directly integrable back to e^(x² + 2). Since there's a ¼ outside,

The answer is just ¼e^(x² + 2) + C, C is a constant

The nice thing about e is that its derivative and integral is also e. It never integrates or differentiates to a sine or a cosine.

In this case, xe^(x2 + 2) does not contain trigonometric functions. Therefore, its integral can appear to be some e. However, there is an x in front. What do we do then?

The thing is, the power of e, which in this case is x2 + 2, is not linear. As such, we are unable to integrate e^(x2 + 2) with respect to x. However, this does not mean that multiplying e^(x2 + 2) by a polynomial keeps the expression unintegrable.

To do such questions, the trick is for us to differentiate e^(x2 + 2) on its own, without the x in front. Interestingly enough, differentiating e^(x2 + 2) gives 2x times itself! As mentioned previously, no trigonometric function appears at all. However, e reappears once again, this time along with an x.

This is how we do such questions.

In short, an expression in the form

k f’(x) f(x)

integrates into

k f(x)

plus an arbitrary constant.

It takes some observation to get used to the derivatives of different expressions using the chain rule. Once you have seen sufficient results for the derivative, such integration questions become easier to solve.