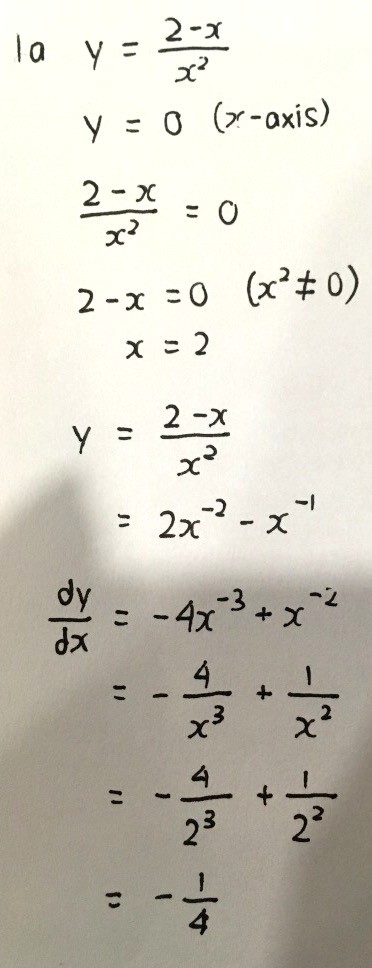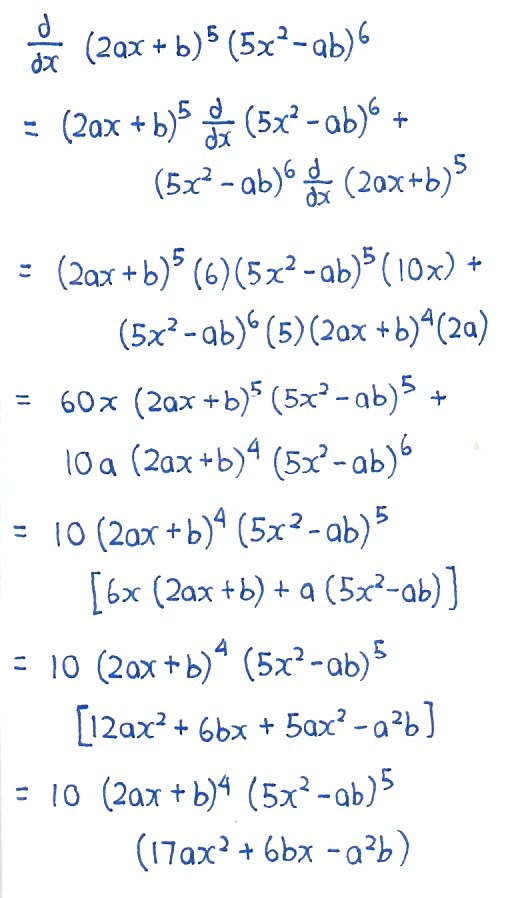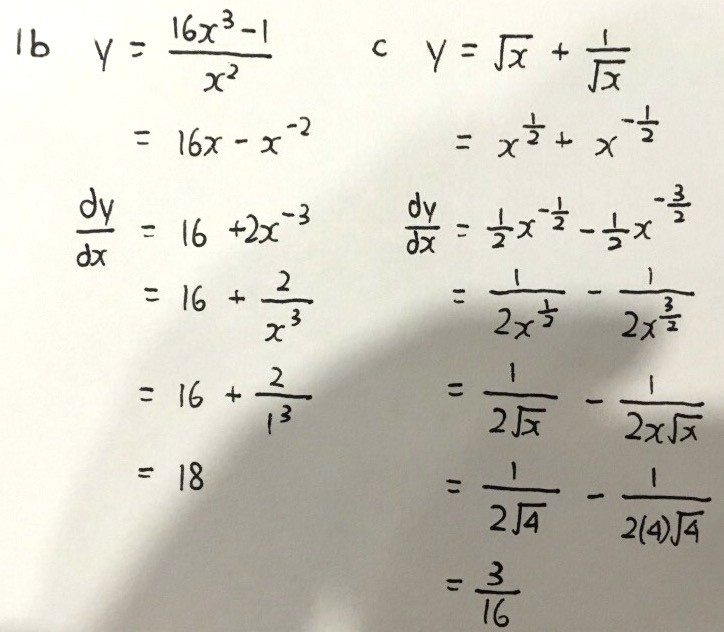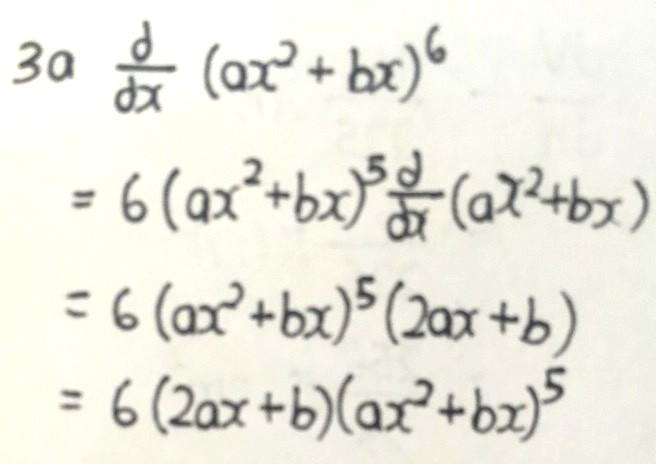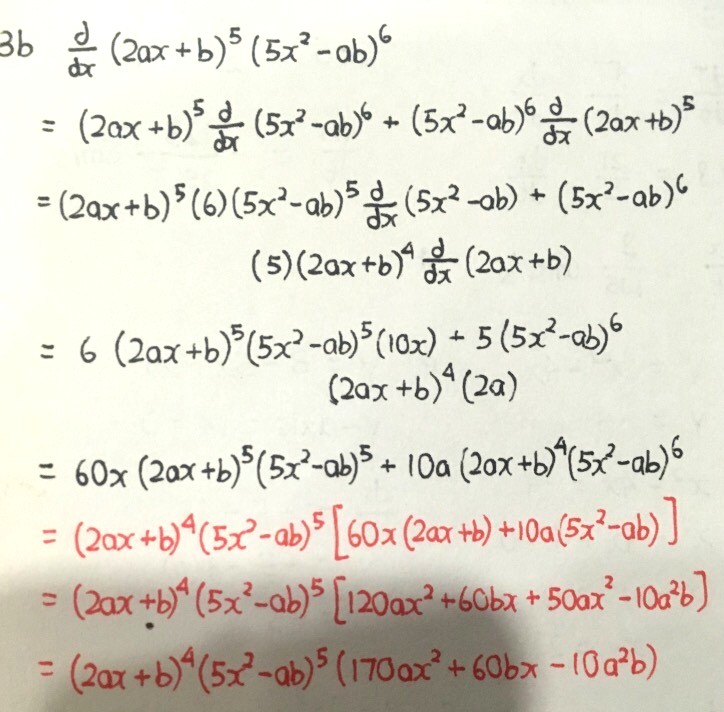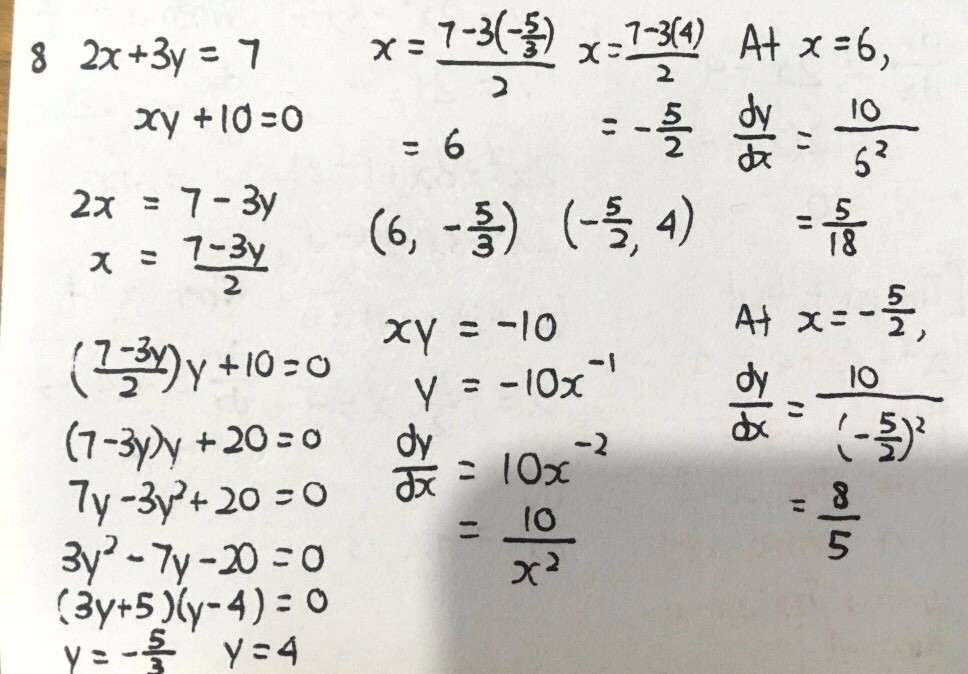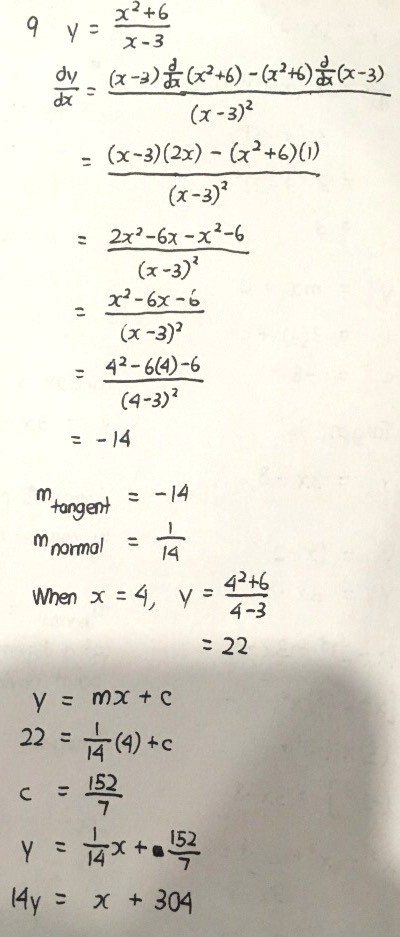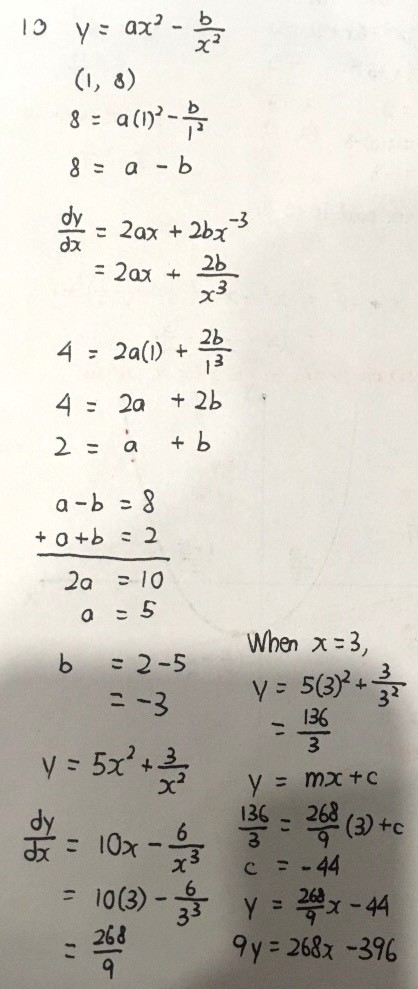Slowly doing, still giving tuition

Got someone downvoted you.
I give u good le

Oh, it doesn’t really matter to me, you can post the next question first, I will see your questions when I am ready

After this will be your maxima and minima, this one there is more things to remember, I summarise them here first

Stationary points —> dy/dx = 0, solve for the coordinates

Remember that dy/dx is gradient at a point, this sounds superficial but it’s important when doing the first derivative test to determine whether the stationary point is a minimum, a maximum or something called inflection.

Second derivative test is an alternative way, using an entirely different approach altogether.

All these will be seen in the next part of differentiation.

ok

I will answer questions later during my tuition in the evening

Today I had nothing to post, tomorrow I posting the new chapter

Ok

Here is a timetable guideline for the last few topics.

June: Maxima/minima,
First half of July: Differentiation for trigo, exponential and logarithm
Second half: revision, basic integration
August: Areas under graphs, integration of trigo and exponential, kinematics

I want try finish all by end of july

Your qns 3b is wrong ah