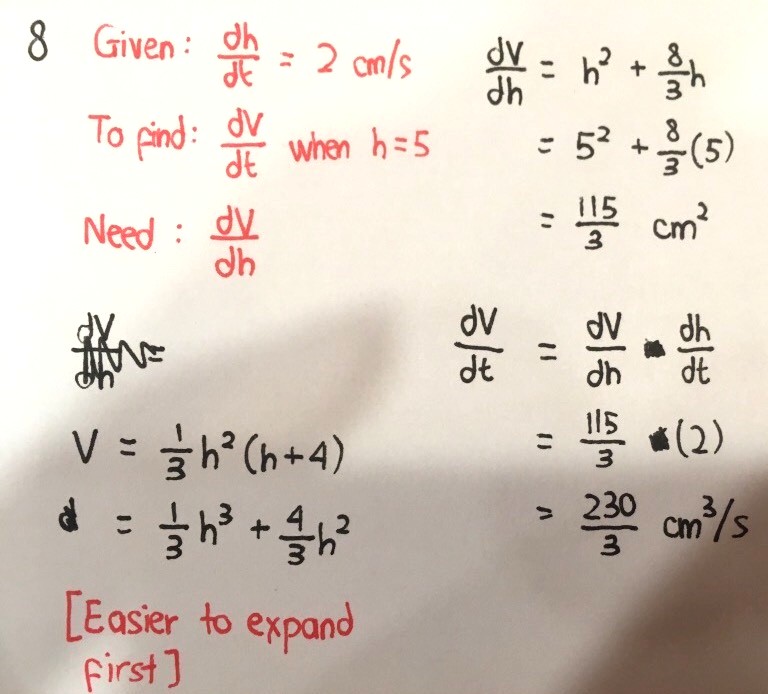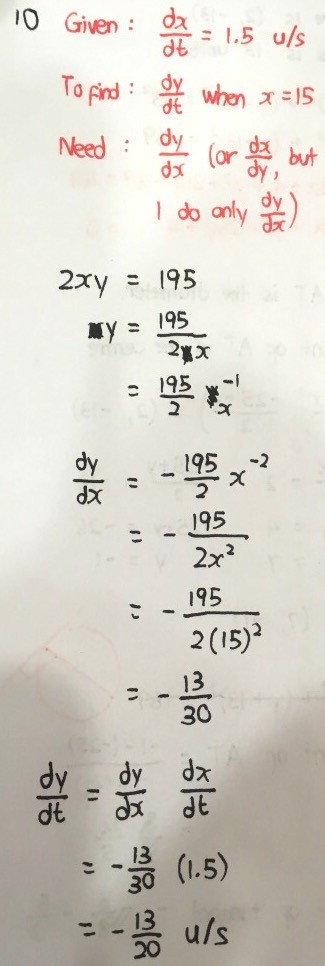Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 4 | A Maths
7 Answers Below
Anyone can contribute an answer, even non-tutors.
Thank you
Date Posted: 4 years ago
Views: 356
You can post the next one, I am free to write now even while I am in the middle of tuition
See 7 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
I hope this solution helps you!
Date Posted:
4 years ago
I can’t even see it
Will do my posting later on a question by question basis in the middle of my tuition
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Q8
Kathy, this topic is basically understanding how things change with time, since rate is related to the time t. We use chain rule formulas involving t, such as dV/dt = dV/dh dh/dt to solve such questions.
The steps to solve this question are as follows.
1. Extract out useful information and transform them into words. Here, the depth increases at 2 cm/s, so we transform it to dh/dt = 2 cm/s.
2. We find out what our wanted quantity is. Here, it’s dV/dt.
3. We express dV/dt in terms of dV, dh and dt. Here, it’s dV/dt = dV/dh dh/dt (think of this as “cross multiplication”), so we need to find out what dV/dh is. It’s the rate of change of V with respect to h, so we need to know what V is in terms of h. It’s given in this question. At other times, you need to form your own equation (such as area of a circle A = #r2).
4. Finally, multiply them out to get the value.
Kathy, this topic is basically understanding how things change with time, since rate is related to the time t. We use chain rule formulas involving t, such as dV/dt = dV/dh dh/dt to solve such questions.
The steps to solve this question are as follows.
1. Extract out useful information and transform them into words. Here, the depth increases at 2 cm/s, so we transform it to dh/dt = 2 cm/s.
2. We find out what our wanted quantity is. Here, it’s dV/dt.
3. We express dV/dt in terms of dV, dh and dt. Here, it’s dV/dt = dV/dh dh/dt (think of this as “cross multiplication”), so we need to find out what dV/dh is. It’s the rate of change of V with respect to h, so we need to know what V is in terms of h. It’s given in this question. At other times, you need to form your own equation (such as area of a circle A = #r2).
4. Finally, multiply them out to get the value.
Date Posted:
4 years ago
Kathy, my phone is ok already so I can continue to help you do some questions.
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Two almost symmetrical approaches to solve Q9
Date Posted:
4 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Q10
Date Posted:
4 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Q11
The fact that V = 8x2 and not some x3 shows that the volume of the cuboid only depends on the dimensions of the base, while the height is fixed at 8 cm.
The fact that V = 8x2 and not some x3 shows that the volume of the cuboid only depends on the dimensions of the base, while the height is fixed at 8 cm.
Date Posted:
4 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Q12
Date Posted:
4 years ago
360 Tutoring Program