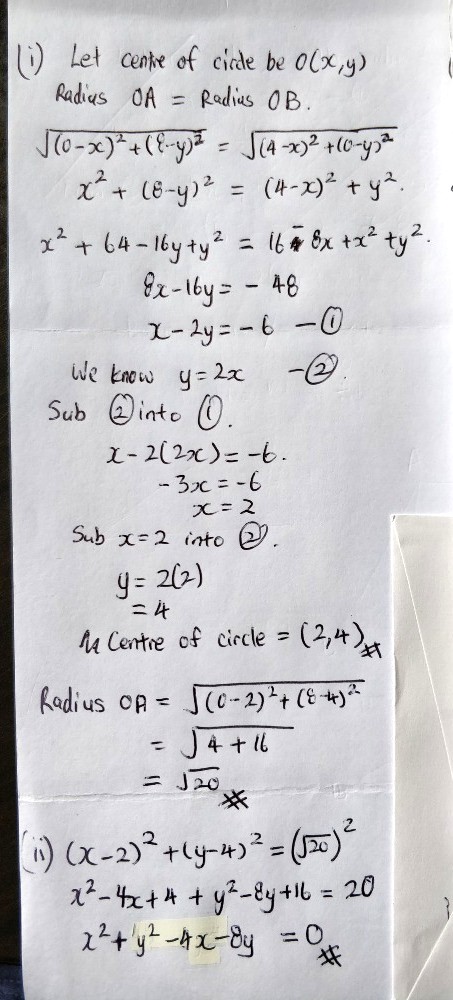Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 4 | A Maths
6 Answers Below
Anyone can contribute an answer, even non-tutors.
Please help me with this qns! Thanks a lot:)
Date Posted: 5 years ago
Views: 347
See 6 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Hi Sonia! Here is my version of the answers for part (i).
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
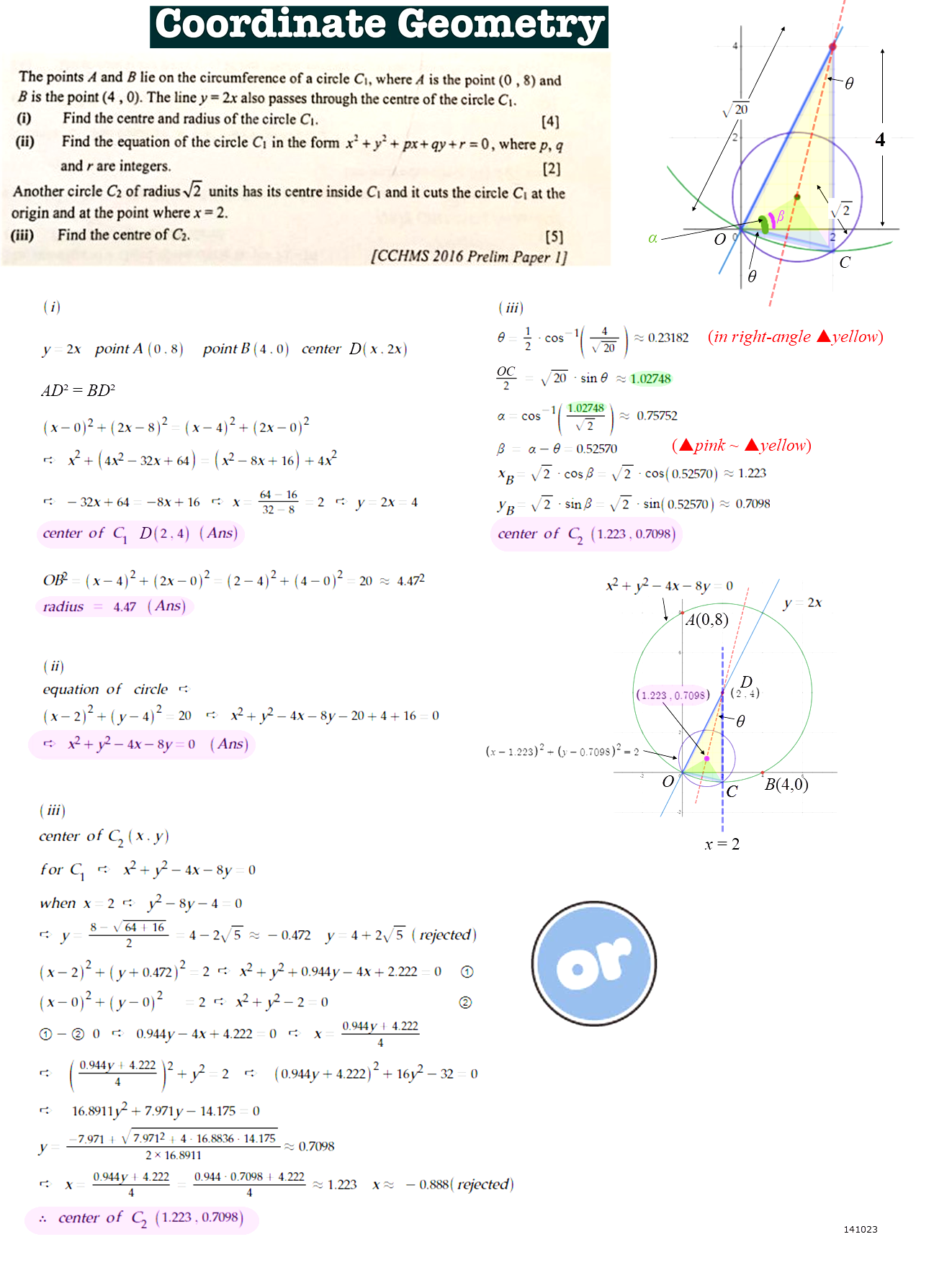
Part (iii), halfway done
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Hi Sonia! I’m sorry for my delayed post. Here is the continuation of my part (iii) working, using trigonometry which the other two tutors have not used. You can use this approach if you wish.
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Last part not difficult, just v tedious
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
I have added the first portion on how to solve it without assuming the mid point. Just an alternative which I thought is interesting.
Date Posted:
5 years ago
It's not an assumption it's a property of circles. The perpendicular bisector of any chord passes through the centre. I used to do it your way when I was in school haha
Oh no, don't get me wrong. Because it wasn't stated that the points are opposite, so I thought it wasn't as suitable to just directly get the mid point using that formula, as it might be 2 points forming a chord. But as you mention, it is a coincidence.
I do agree with you that the perpendicular bisector is the more efficient method. I tried doing with the radius method for part iii and it was hell. Great way of solving.
I do agree with you that the perpendicular bisector is the more efficient method. I tried doing with the radius method for part iii and it was hell. Great way of solving.
The proof of this property requires some congruency of triangles and some reasoning.
There is yet a third method which involves several simultaneous equations, so if a student does not realise this property, he/she can still solve the question based on other approaches.
360 Tutoring Program