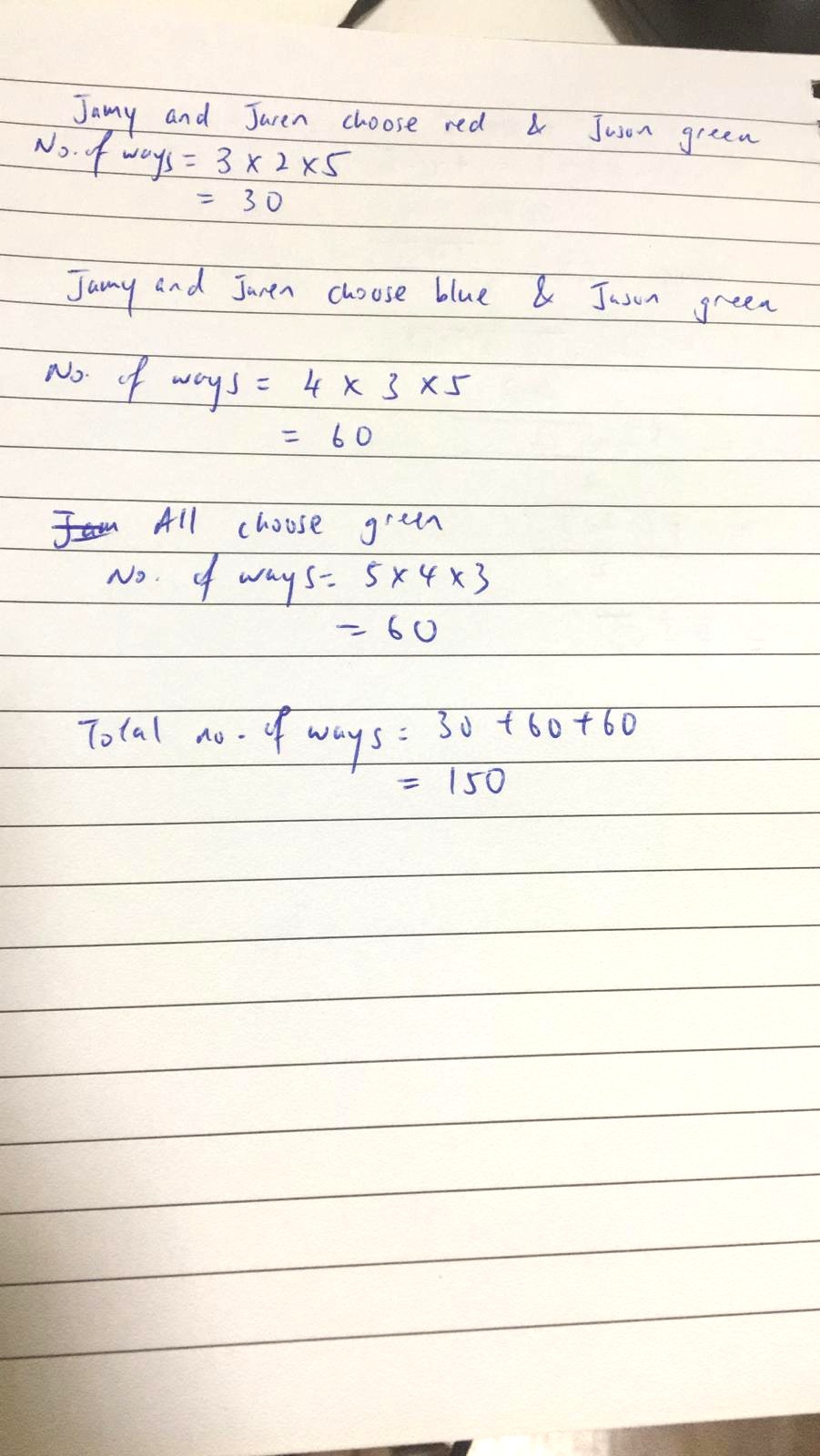12 marbles : 3 red, 4 blue, 5 green.

Assign one green marble to James first.

11 marbles are left : 3 red, 4 blue, 4 green



Case ① : Jamy and Jaren both get green.
9 marbles are left : 3 red, 4 blue, 2 green

Number of ways to distribute the 9 remaining marbles to the other 9 children
= 9! ÷ 3! ÷ 4! ÷ 2! = 1260


Case ② : Jamy and Jaren both get red.
9 marbles are left : 1 red, 4 blue, 4 green

Number of ways to distribute the 9 remaining marbles to the other 9 children
= 9! ÷ 1! ÷ 4! ÷ 4! = 630

Case ③ : Jamy and Jaren both get blue.
9 marbles are left : 3 red, 2 blue, 4 green

Number of ways to distribute the 9 remaining marbles to the other 9 children
= 9! ÷ 3! ÷ 2! ÷ 4! = 1260

Total of the three cases = 1260 + 630 + 1260 = 3150

Three cases to consider.

1. Jason receives a green marble, the other two receive red marbles and the rest of the class receive what is left over.

2. Jason receives a green marble, the other two receive blue marbles and the rest of the class receive what is left over.

3. The three of them receive green marbles, the rest of the class receive what is left over.

1. Jason green (1 way), the other two red marbles (1 way), and the rest receive the left-overs of 1 red marble, 4 blue marbles and 4 green marbles.

This can be done in a total of 9! divided by 4! divided by 4! ways.

The other two cases follow similar approaches.

Add the values for the three cases and you have the total number of possible ways.