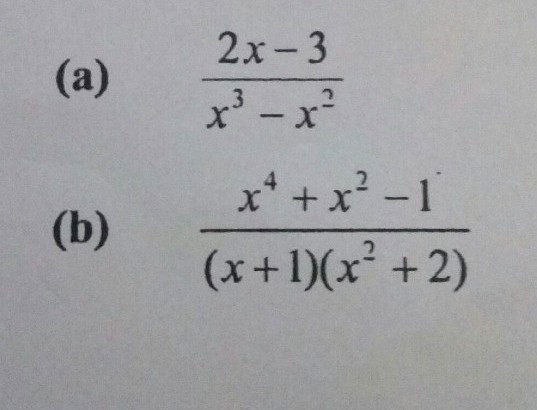Use repeated linear

As far as we can factorise the expressions in the denominator, do so. This is to get a form as simple as possible.

Suppose the denominator contains x + 5 and x2 + x - 2. Technically what we can do is to place A on top of x + 5 and Bx + C on top of x2 + x - 2 (always put the numerator as one degree lower than the denominator). This is not wrong at all.

However, upon inspection, we know that x2 + x - 2 = (x + 2) (x - 1), which means that the second fraction (Bx + C) / (x2 + x - 2) can actually be decomposed further.

This is the reason why we strive to simplify the denominator as far as possible. Only when we face quadratic terms such as x2 + 3 which cannot be factorised at all, then we have no choice but to leave x2 + 3 as it is (and put the numerator as one degree lower i.e. a linear term like Px + Q).

In the case of x3 - x2, we can factorise the denominator into x2 (x - 1) which in other words is the same as x times x times (x - 1). There are two repeated terms x and one isolated term (x - 1). This involves a case of both repeated linear roots (since the linear factors x appears more than once in the denominator) and non-repeated linear roots (since there exists the other term x - 1).

In this case, for the repeated linear term x2, the partial fraction that we will obtain will include A / x and B / x2. The repeated term to the power of 1 and the repeated term to the power of 2. If there are more than two terms which are repeated, then there will be something like A / x + B / x2 + C / x3, but this scenario is not within the A Maths syllabus.

Lastly, always remember to start off by checking whether a given fraction is proper or improper, because having improper fractions would mean that long division needs to be performed first before the resulting proper fraction can be decomposed into their respective partial fractions.