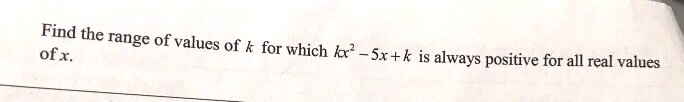The other tutor's workings are fully correct and logical.

Now, we are trying to find the range of values of k for which kx2 - 5x + k is always positive for all real values of x. This is equivalent to saying that the curve y = kx2 - 5x + k lies completely above the line y = 0 (the x-axis).

The key word here is, "all real values of x". This means that whatever the case, the curve will be 'always positive', or equivalently, the curve will always lie above the x-axis.

If the curve always lies above the x-axis, the curve will never touch the x-axis. As a result, the equation kx2 - 5x + k can never equal 0, since it is always positive after all. This equates to the equation having no real roots, or b2 - 4ac < 0.

Additionally, for a curve to be 'always positive', the coefficient of x2 (k in this case) must be positive since only smiley face curves are capable of being 'always positive'.

From there, b2 - 4ac < 0.

(-5)^2 - 4 (k) (k) < 0
25 - 4k2 < 0
4k2 - 25 > 0
(2k + 5) (2k - 5) > 0

At this point, you need to draw the quadratic graph for the b2 - 4ac (this is different from the actual quadratic graph which does not touch the x-axis at all).

Once you solve this inequality, you should get k < -2.5 or k > 2.5.

Only smiley face graphs can be always positive (sad face can never be always positive), so k < -2.5 has to be rejected. So the range is k > 2.5.

If you have further queries let me know.

These are the important conditions for a curve which is always positive for all real values of x:

1. b2 - 4ac < 0 (because the curve will never touch the x-axis at all)
2. a > 0

These are the important conditions for a curve which is always negative for all real values of x:

1. b2 - 4ac < 0 (because the curve will bever touch the x-axis at all)
2. a < 0

This type of question 'find the range of values of k for which ... for all real values of x' is to be distinguished from 'find the range of values of x for which...' which is a mere inequality question rather than a b2 - 4ac question.

May i ask why we cant draw the graph as curving upwards so since the discriminant is <0, thus the solution is -5/2 < k < 5/2

I made that same error initially.

There are two graphs to consider for the entire question.

The first graph is the actual graph, which is obviously a smiley face graph with a turning point above the x-axis since the curve is always positive.

We know that the graph does not touch the x-axis at all, and hence, there are no real roots, or b2 - 4ac < 0.

We find that 25 - 4k2 < 0 after simplifying the above inequality. Now at this point, we need to draw yet another quadratic graph for this 25 - 4k2, which should cut the horizontal at two points.

Of course, 25 - 4k2 is a sad face graph which goes up and then down as per what the other tutor has drawn. Of course, the regions in which 25 - 4k2 < 0 are the regions where k < -2.5 or k > 2.5; the middle region is the part where the sad face graph goes above the horizontal line. Hence, the solution to the inequality is k < -2.5, k > 2.5.

Personally, I prefer converting the inequality to 4k2 - 25 > 0 (you have learnt the rules on inequalities in E Maths right?). This becomes a smiley face graph. Once you draw this one out, you will realise that the regions in which 4k2 - 25 > 0 are the regions where k < -2.5 or k > 2.5, as before.

This would be the method to approach the inequality that arises after simplification of the discriminant b2 - 4ac.

In solving such quadratic inequalities, I always like to make the coefficient of x2 (or the squared variable) positive so that I only deal with smiley face graphs. The inequality arising from b2 - 4ac < 0 does not have to necessarily end with the < sign, as per my method where I converted 25 - 4k2 < 0 into 4k2 - 25 > 0 which I am personally more comfortable with.

The statement b2 - 4ac < 0 just simply relates to the condition that the curve does not intersect a given line (x-axis for example). Once you have input the expressions for a, b and c, the resulting equation becomes an ordinary inequality question to solve (as though the question started out as a normal inequality question “Solve the quadratic inequality 25 - 4k2 < 0”). You have learnt how to solve quadratic inequalities right?

I understand, thank you so much for ur help!