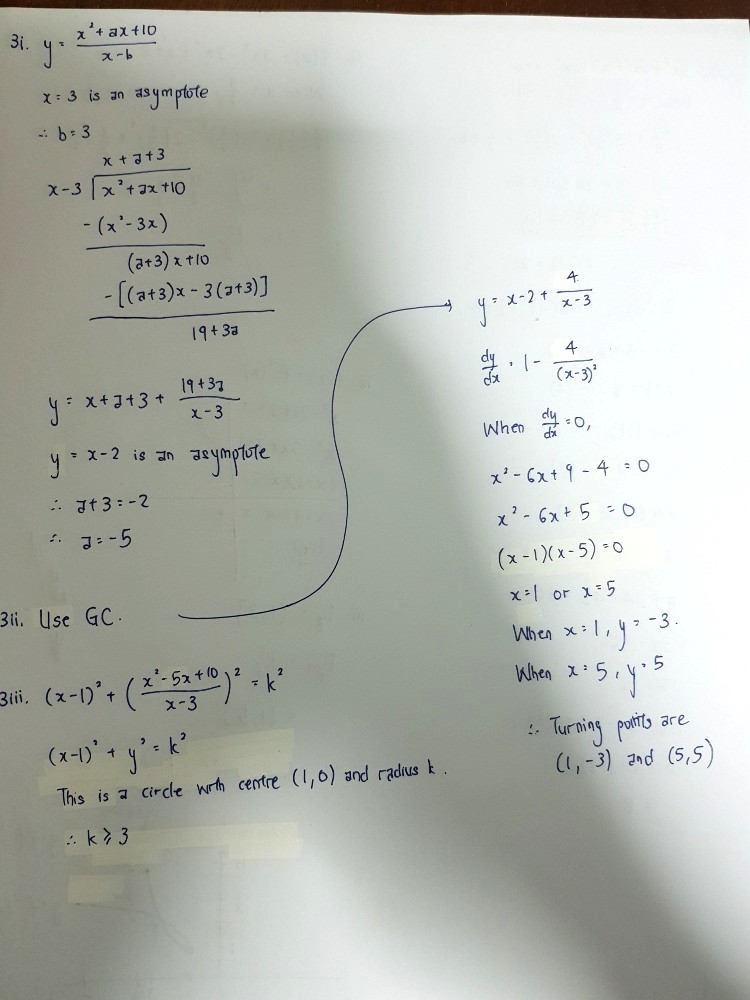if x = b , denominator = 0. Then the function becomes undefined.

So the vertical asymptote is x = b since x ≠ b (graph does not touch or cut the asymptote)

Thus b = 3

So y = (x² + ax + 10)/(x-3)

Since oblique asymptote is y = x - 2, when
(x² + ax + 10) divided by (x-3), x - 2 is the quotient.

The graph can be represented in the form
y = x - 2 + c/(x-3), c is a constant and c/(x-3) is the remainder.

(Degree of remainder is at least 1 less than divisor. Since degree of divisor is 1, degree of remainder = 0. So the remainder is a constant with no term of x)

y = (x-2)(x-3)/(x-3) + c/(x-3)

y = (x² - 5x + 6 + c)/(x-3)

Comparing coefficients, a = -5

((x² - 5x + 10)/(x-3))² + (x - 1)² = k²

Observe that since k is a positive constant,
k² > 0

So ((x² - 5x + 10)/(x-3))² + (x - 1)² > 0


From the graph in part ii), the curve does not cut the x-axis. So y ≠ 0.

And the turning points are a maximum point (-1,3) and a minimum point (5,5).

So (x² - 5x + 10)/(x-3) ≥ 5 and x² - 5x + 10)/(x-3) ≤ - 3

However, when we square the expression, the y-values all become positive. The maximum point becomes a minimum point (1,(-3)²) = (1,9)

So now ((x² - 5x + 10)/(x-3))² ≥ 9 since all other points on the curve have a larger y value than (1,9)

(x-1)² ≥ 0 . When x = 1, (x-1)² = 0 and ((x² - 5x + 10)/(x-3))² = 9. So both expressions are at their minimum value.

Thus, ((x² - 5x + 10)/(x-3))² + (x - 1)² ≥ 9

((x² - 5x + 10)/(x-3))² + (x - 1)² ≥ 3²

Thus k ≥ 3