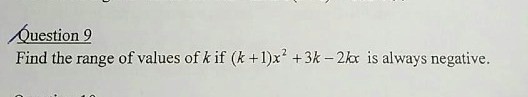Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
This question need another answer.

idk how to do
To distinguish the two cases, we look at the coefficient of x2. ‘Always positive’ graphs can only be exhibited by smiley face graphs, or a > 0. Similarly, ‘always negative’ graphs can only be exhibited by sad face graphs, or a < 0.
Whenever you see a question like ‘find the range of values of k (note: not x) for which the curve is always positive for all real values of x’, this means the graph will never cut the x-axis at all, so you must immediately identify that b2 - 4ac < 0 (and a > 0).
See 1 Answer
Being fully below the x-axis means that the curve will not ever cut the x-axis. In turn, this means that there are no solutions to the equation y = 0. No solutions means no real roots; hence, b2 - 4ac must be < 0.
You will need to find out what a, b and c are from the equation. Here, a = k + 1, b = -2k and c = 3k. From there, you will need to form an inequality and solve for the inequality. Note that multiplying or dividing both sides of an inequality by a negative number changes the sign of the inequality (you will need to have the necessary knowledge from E Maths first).
You will need to bear in mind that only sad face graphs can be 'always negative'. We look at the coefficient of x2 to identify whether a graph is smiley face or sad face. For sad face graphs, the coefficient must be a negative number. In other words, a < 0, or in this case, k + 1 < 0. Where necessary (it does happen in this question eventually), we will need to reject some values of k.