Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
Secondary 1 | Maths
2 Answers Below
Anyone can contribute an answer, even non-tutors.

I m stuck,i first got it but i forget what it is!
Please help and tell me where i went wrong. Thanks
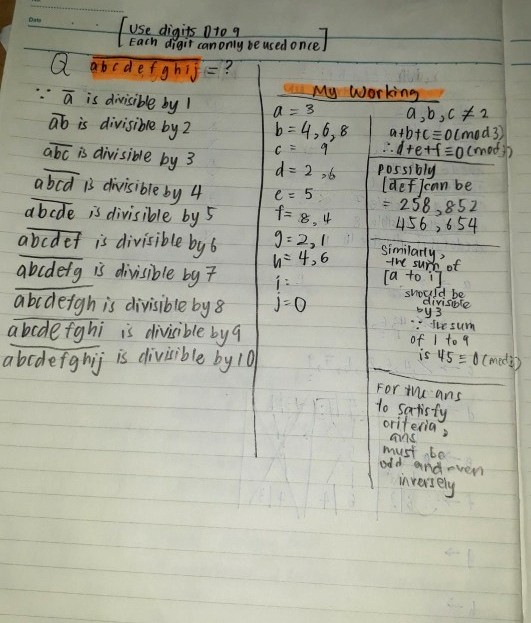
Note that all digits 1 to 9 are used and r not repeated.
From condition 10, we know that j equals 0
From conditions 2, 4, 6 and 8, we know that b, d, f, h are even numbers, therefore a, c, g, i are 1, 3, 7, 9 in some order.
Furthermore, from conditions 4 and 8 we know that cd is divisible by 4 and gh is divisible by 8 (because fgh is divisible by 8 and f is even). Because c and g are odd, d and h must be 2 and 6 in some order.
From conditions 3 and 6, we know that a+b+c, d+e+f, g+h+i are all divisible by 3.
If d=2, then f=8, h=6, b=4. a+4+c is divisible by 3, therefore a and c must be 1 and 7 in some order, g and i must be 3 and 9 in some order. g6 is divisible by 8, therefore g=9. But neither 1472589 nor 7412589 is divisible by 7.
Therefore d=6, and f=4, h=2, b=8. g2 is divisible by 8, therefore g=3 or 7. a+8+c is divisible by 3, therefore one of a and c is chosen from 1 and 7, the other is chosen from 3 and 9.
If g=3, then one of a and c is 9, the other is chosen from 1 and 7. But none of 1896543, 7896543, 9816543 and 9876543 is divisible by 7.
Therefore g=7, one of a and c is 1, the other is chosen from 3 and 9. From 1836547, 1896547, 3816547 and 9816547, only 3816547 is divisible by 7 (the quotient is 545221).
Therefore, the number we are looking for is 3816547290.
See 2 Answers