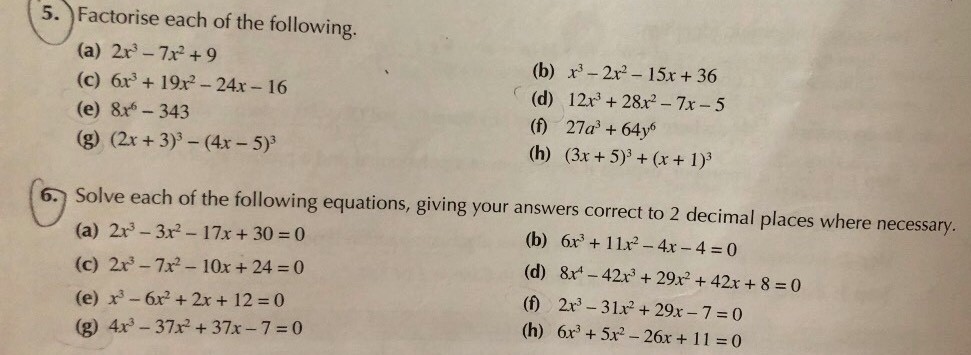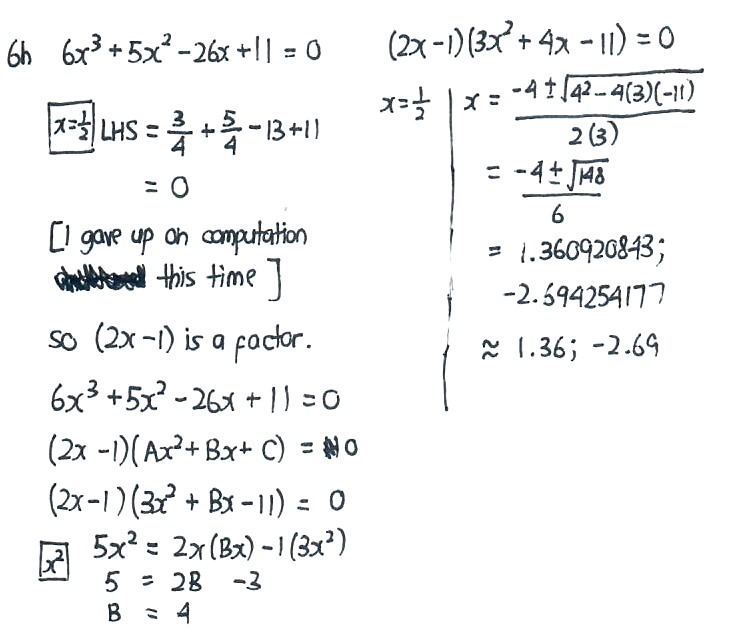Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
secondary 4 | A Maths
4 Answers Below
Anyone can contribute an answer, even non-tutors.
Thank you
Date Posted: 5 years ago
Views: 570
See 4 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
5a to 5g
Will do the rest at a later time when I can spare the time.
Will do the rest at a later time when I can spare the time.
Date Posted:
5 years ago
Can I know if I don’t u test out to find the factor got any way to do it
Thank you so much pls help ah
At the secondary level, this test out of a factor is the ONLY way to factorise the expression.
Unlike quadratic expressions, cubic expressions are much harder to factorise (or even to spot the pattern at all). Only a small minority of such cubic equations can be factorised by observation and grouping of terms (in a very similar way to factorising ab + ac + bd + cd by grouping expressions into twos).
Once you proceed to polynomials of degree 4 and more, factorising gets even harder.
Fortunately for your exams, the expressions are factorisable with at least one number which is guessable. And the numbers to guess are predictable. Typically, the numbers to guess are factors of the constant term (and their negatives). For example, if the constant term is 30 or -30 (eg x3 - 29x + 30 or x3 - 29x - 30), then the numbers to guess are 1, 2, 3, 5, 6, 10, 15, 30 and their negatives. Guessing of fractions such as 1/2 is more difficult, but should not be seen in exams at all.
There is another method to do this, but it's way beyond the secondary level and I have no idea how to execute the other method at all (it's way too advanced for me).
I am currently working on the remaining questions which will take me another 45 mins to complete.
Unlike quadratic expressions, cubic expressions are much harder to factorise (or even to spot the pattern at all). Only a small minority of such cubic equations can be factorised by observation and grouping of terms (in a very similar way to factorising ab + ac + bd + cd by grouping expressions into twos).
Once you proceed to polynomials of degree 4 and more, factorising gets even harder.
Fortunately for your exams, the expressions are factorisable with at least one number which is guessable. And the numbers to guess are predictable. Typically, the numbers to guess are factors of the constant term (and their negatives). For example, if the constant term is 30 or -30 (eg x3 - 29x + 30 or x3 - 29x - 30), then the numbers to guess are 1, 2, 3, 5, 6, 10, 15, 30 and their negatives. Guessing of fractions such as 1/2 is more difficult, but should not be seen in exams at all.
There is another method to do this, but it's way beyond the secondary level and I have no idea how to execute the other method at all (it's way too advanced for me).
I am currently working on the remaining questions which will take me another 45 mins to complete.
In the exams, there is at least ONE guessable integer factor. The other factors may be unguessable or do not even exist (a cubic equation can have one, two or three solutions).
For e and f I can’t understand
For e and f, there is a special factorisation formula for it:
a3 + b3 = (a + b) (a2 - ab + b2)
a3 - b3 = (a - b) (a2 + ab + b2)
where I recognise that the two terms there can be expressed as cubes.
Take 8x6 - 343 for example.
If you identify 8x6 as (2x2)^3 and 343 as 7^3, then you would be able to factorise them using the above formula, noting that a = 2x2 and b = 7. Then you can replace the a in the formula by 2x2 and the b by 7.
It's the same idea to factorise terms like a2 - b2 = (a + b) (a - b) where you recognise the difference of two 'perfect squares'.
You can also factorise the expression the normal way by guessing numbers as well, but possibly much harder (and I am very sure that the number to guess here is not an integer).
a3 + b3 = (a + b) (a2 - ab + b2)
a3 - b3 = (a - b) (a2 + ab + b2)
where I recognise that the two terms there can be expressed as cubes.
Take 8x6 - 343 for example.
If you identify 8x6 as (2x2)^3 and 343 as 7^3, then you would be able to factorise them using the above formula, noting that a = 2x2 and b = 7. Then you can replace the a in the formula by 2x2 and the b by 7.
It's the same idea to factorise terms like a2 - b2 = (a + b) (a - b) where you recognise the difference of two 'perfect squares'.
You can also factorise the expression the normal way by guessing numbers as well, but possibly much harder (and I am very sure that the number to guess here is not an integer).
Ok. Understand,
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
6d, 6e, 6f, 6g.
6f and 6g are not exactly in your syllabus as fractional guesses are required.
I will remain online until around 1 am.
6f and 6g are not exactly in your syllabus as fractional guesses are required.
I will remain online until around 1 am.
Date Posted:
5 years ago
Ok thank you so much
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
6h, which again requires fractional guess.
Also, an important note is that the quadratic expression which you factor out may not have any solutions at all. Do not be surprised if no solutions appear out of the quadratic expression.
Also, an important note is that the quadratic expression which you factor out may not have any solutions at all. Do not be surprised if no solutions appear out of the quadratic expression.
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
5h, 6a, 6b, 6c
(Lack of space on paper)
(Lack of space on paper)
Date Posted:
5 years ago
Only one way to do this?
For question 6, the first thing to do is to guess (the only way at your level).
Subsequently, to obtain the Ax2 + Bx + C, you can perform different things, any one of this
- Long division
- Comparing coefficients (which I have used)
- Sub in random x like you would for solving identities (after all, both sides are identities since we are just factorising from the LHS to the RHS). This method is the hardest of the three.
Subsequently, to obtain the Ax2 + Bx + C, you can perform different things, any one of this
- Long division
- Comparing coefficients (which I have used)
- Sub in random x like you would for solving identities (after all, both sides are identities since we are just factorising from the LHS to the RHS). This method is the hardest of the three.
If Guess wrongly how?
So in 6a, my first try was x = 1, and it leads to LHS not equal to RHS, so x = 1 does not work.
I moved on to x = 2 and found that x = 2 works. Had it not worked, I would have needed to try other numbers (may be even up to x = -30).
Typically the numbers are factors of the constant term.
For your syllabus, at least one of these integer number guesses must work. The exams will not ask questions which does not meet this criteria.
I moved on to x = 2 and found that x = 2 works. Had it not worked, I would have needed to try other numbers (may be even up to x = -30).
Typically the numbers are factors of the constant term.
For your syllabus, at least one of these integer number guesses must work. The exams will not ask questions which does not meet this criteria.
Ok thanks.
Can help more tonight, having a test this Friday
Can help more tonight, having a test this Friday
360 Tutoring Program