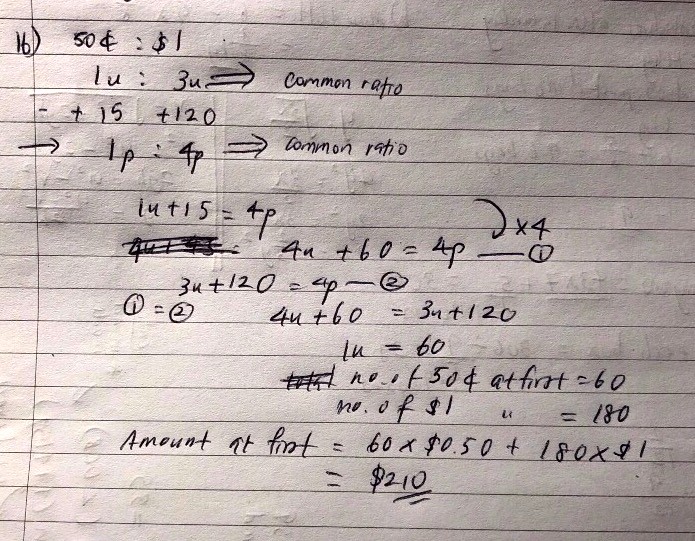May i know u based on what theory that they are equal? I understood the multples are equal, but the question did not mention anything about equal.. tks

The method is perfectly logical and fully correct (except for an early miswriting of a number).

Initially the ratio 50c to 100c is 1 : 3. We do not know the EXACT number of each type of coins at first, but we do know that the ratio is 1 : 3.

In other words, there are three times as many 100c coins as 50c coins, so if there are 'u' 50c coins at first, there must be three times as many 100c coins , or simply put, '3u' 100c coins at first. The letter 'u' here simply represents 'units'.

Number of 50c coins before: u
Number of 100c coins before: 3u

----------------------------------------------

Now, if you have worked out the maths later, you will realise that there are 4 times as many 100c coins as 50c coins. The number of coins of each type has changed already, so we use another letter 'p' this time.

Number of 50c coins after: p
Number of 100c coins after: 4p

Remember that the values of u and p are not the same.

----------------------------------------------

In the process from 'before' to 'after', 15 pieces of 50c coins and 120 pieces of 100c coins are added.

Number of 50c coins before: u
Number of 50c coins after: p

Since 15 pieces of 50c coins were added, u + 15 = p.

Number of 100c coins before: 3u
Number of 100c coins after: 4p

Since 120 pieces of 100c coins were added, 3u + 120 = 4p.

----------------------------------------------

So now we have two equations.

u + 15 = p
3u + 120 = 4p

----------------------------------------------


If p is 15 more than u, then 2 times of p will be 30 more than 2 times of u, correct? Similarly, 4 times of p will be 60 more than 4 times of u.

4u + 60 = 4p

But we also know that 3u + 120 = 4p. Both the '4p' terms are referring to the same thing.

This means that 4u + 60 = 3u + 120.

4 units + 60 = 3 units + 120

If you draw your model diagram here, you will find that 1 'u' = 60 pieces. Remember that 'u' represents the number of 50c coins at first.

So there must have been 60 pieces of 50c coins and 180 pieces of 100c coins at first.

You can calculate the total value of all these coins from there on.

This technique of solving equations is known as the simultaneous equations in two variables, which will be used very frequently in Secondary 2 or 3.

Hi, Thank for yr explanation.