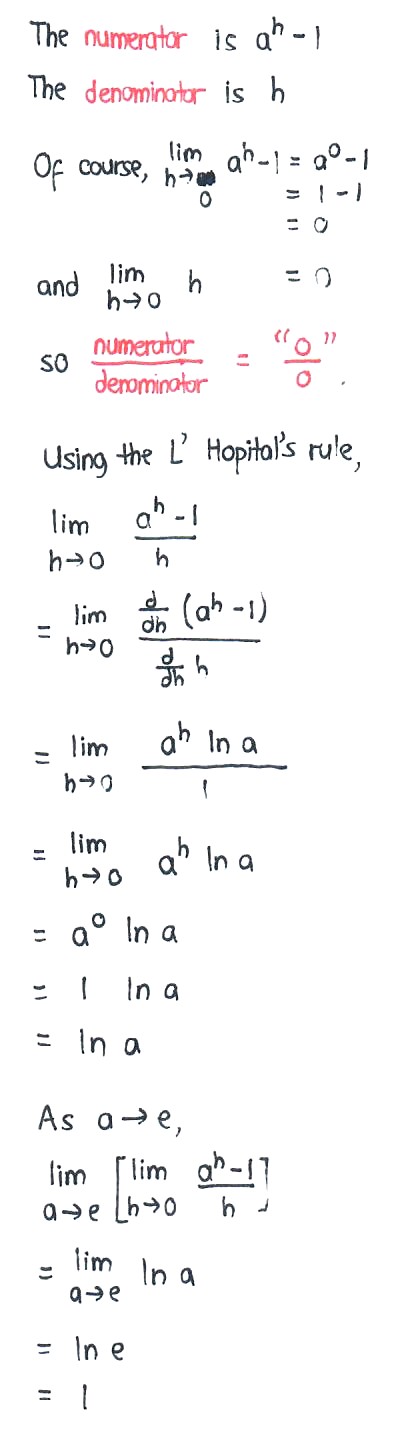Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
|
2 Answers Below
Anyone can contribute an answer, even non-tutors.

how to solve this two question?
So (1 + h) → 1
And thus (1 + h)^h → 1
for the 2nd one, apply L'Hopital's rule. Differentiate both numerator and denominator.
So lim (a^h -1)/h = lim a^h ln(a) / 1
= a^h ln (a)
As h→0, a^h → 1
So a^h ln (a) → ln (a)
Now, since a →e, ln (a) → ln (e) = 1
So the limit is 1
See 2 Answers
L' Hopital's rule can be invoked when the value of
Numerator/Denominator
is either 0/0 or infinity/infinity.
If the first application of the L' Hopital's rule still results in either 0/0 or infinity/infinity, we must do another application of the L' Hopital rule. This is to be done until the limit is no longer 0/0 or infinity/infinity.