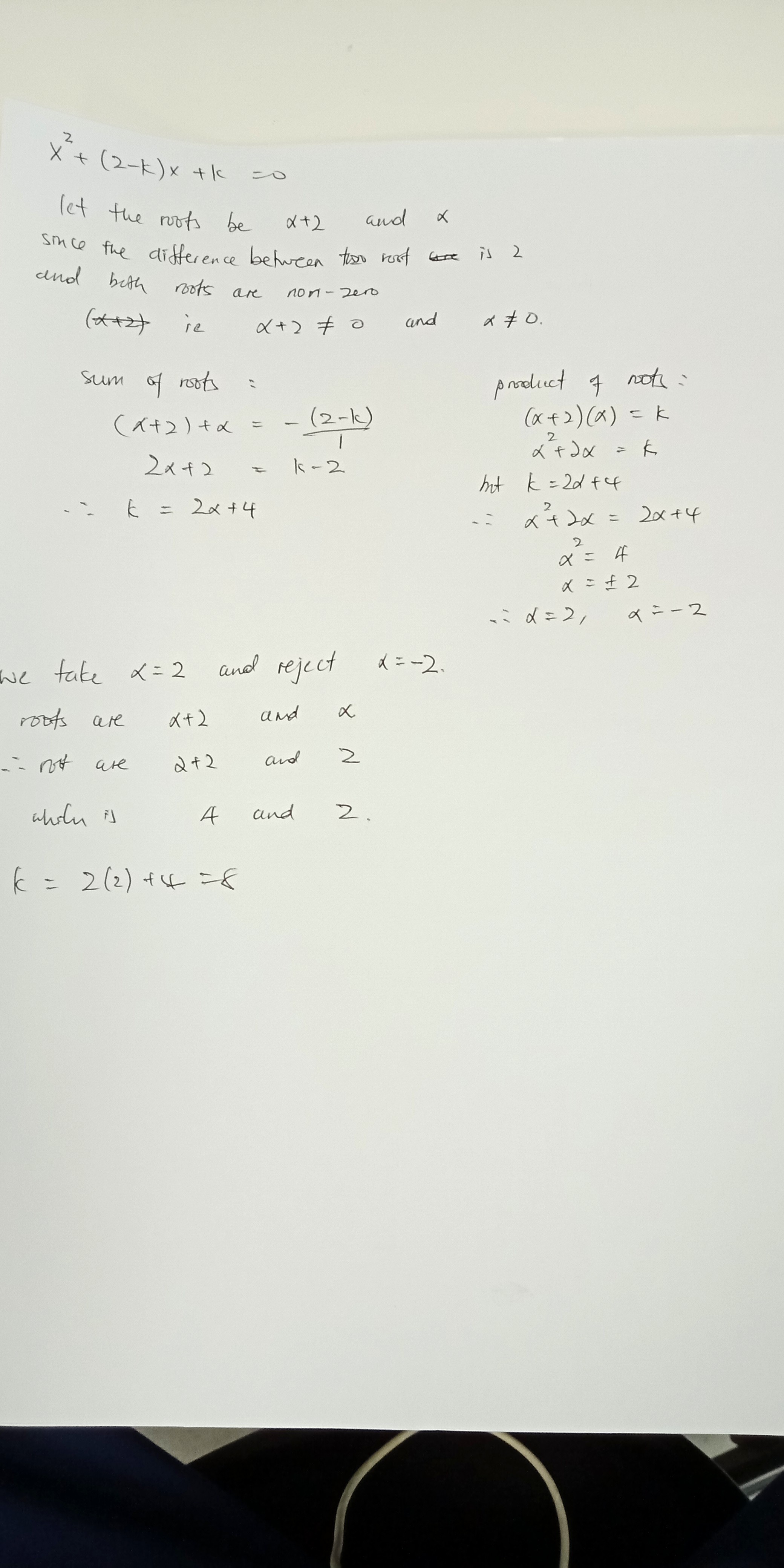Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

i have no idea of how to do this
Therefore, a = 1, b = (2 - k), c = k.
We will now study the quadratic formula, which is -b +- √(b^2 - 4ac) divided by 2.
If √(b^2 - 4ac) = 2, then one root will be -b/2 + 1, and the other root will be -b/2 -1.
The difference between the roots is 2, which is what we are aiming for.
Hence, b^2 - 4ac = 4.
We know the values of a, b and c, so place them in:
(2 - k)^2 - 4k = 4
Expand:
k^2 - 8k + 4 = 4
Subtract 4 on both sides:
k^2 - 8k = 0
We can factorize:
k(k - 8) = 0
k = 0 or k = 8
The roots will be -b/2 +- 1, which is:
-(2 - k)/2 +- 1
When k = 0, the roots are -2, 0.
When k = 8, the roots are 2, 4.
However, we know the quadratic equation has non-zero roots. So k = 0 is rejected.
The final answer is k = 8, the roots are 2, 4.
See 1 Answer