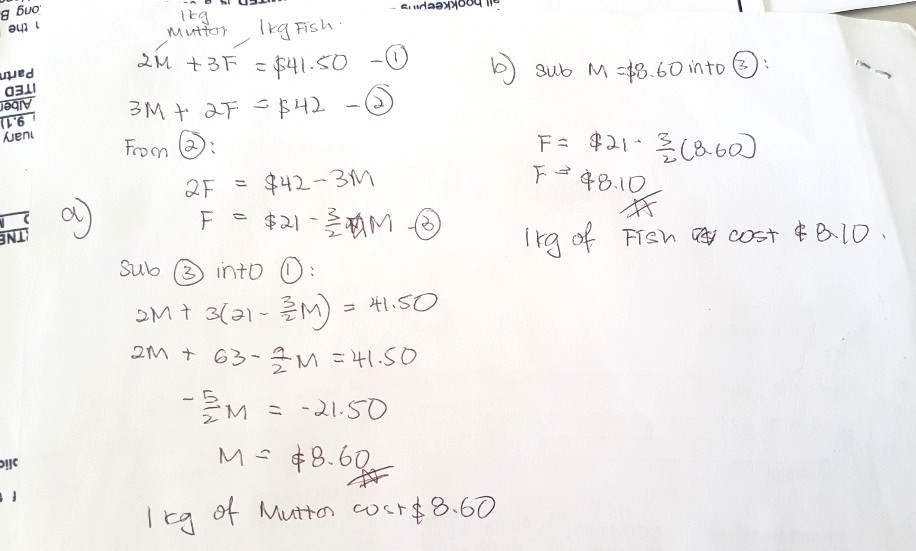Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.
Question
primary 6 | Maths
| Data Analysis
2 Answers Below
Anyone can contribute an answer, even non-tutors.
Please help me. Thanks
Date Posted: 5 years ago
Views: 460
See 2 Answers
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
Hope this helps! I solved it using simultaneous equations.
Date Posted:
5 years ago
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
For this question, a good idea is to find a way to make the number of fish equal in both cases. This involves the lowest common multiple (LCM) of two numbers.
The LCM of 2 and 3 is equal to 6, so we express both cases in terms of 6 kg of fish.
If 3 kg mutton and 2 kg fish cost $42, then three times the amount bought will cost three times as much, so 9 kg mutton and 6 kg fish cost $126.
We do a very similar method for the other case and we see that 4 kg mutton and 6 kg fish cost $83.
The only difference that separates the 9 kg mutton and 6 kg fish from the 4 kg mutton and 6 kg fish is the extra 5 kg of mutton which will cost an extra $43.
From there, we can find the cost of 1 kg of mutton and then the cost of 1 kg of fish.
The LCM of 2 and 3 is equal to 6, so we express both cases in terms of 6 kg of fish.
If 3 kg mutton and 2 kg fish cost $42, then three times the amount bought will cost three times as much, so 9 kg mutton and 6 kg fish cost $126.
We do a very similar method for the other case and we see that 4 kg mutton and 6 kg fish cost $83.
The only difference that separates the 9 kg mutton and 6 kg fish from the 4 kg mutton and 6 kg fish is the extra 5 kg of mutton which will cost an extra $43.
From there, we can find the cost of 1 kg of mutton and then the cost of 1 kg of fish.
Date Posted:
5 years ago
Thanks alot for your help
360 Tutoring Program