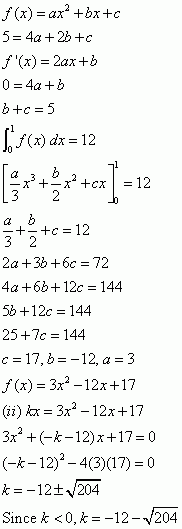Hello. I can't exactly tell the lower and upper bound of the integrals cos it looks blurry, but I will take it as 0 and 1 respectively. With that, here's my approach on this:

A) First find a general integral for the function
f(X)= ax2 + bx + c

It should give you ax3/3 + bx2/2 + cx + d, where d is the constant.

Now substitute X=0 and X=1 separately into the integrated equation. Subtracting one from the other should give you 12.

Integral f(0)= d ------------- (1)
Integral f(1)= a/3 + b/2 + c + d -----------(2)

(2)-(1) = a/3 + b/2 + c = 12 -----------(3)

Now that we have our first equation (3), we can find the other one.

Since we were given the turning point of the equation, we can find the derivative of the equation to find out some details.

F'(x) = 2ax + b

At turning point, f'(2) = 0

0 = 2a(2) + b
b = - 4a ------------ (4)

Substitute (4) into (3),
12= a/3 + (-4a)/2 + c
12 = a/3 - 2a + c
12= c - 5a/3
c = 12 + 5a/3 -------(5)

Now that you have (4) and (5), you can now substitute them into your f(X) equation.

f(X)= ax2 + bx + c
f(X) = ax2 - 4ax + 12 + 5a/3

You have your turning point coordinates, substitute them into the equation f(X) = 5, X=2

5 = a(2)^2 - 4(a)(2) + 5a/3
5 -12 = 4a - 8a + 5a/3
-7 = -7a/3
a = 3 ---------(6)

Substitute (6) into (4) and (5), you will finally get

a=3 b= -12 c = 17

f(X) = 3x2 - 12x + 17


B) At this point of the curve, it only intersects the line y= kx at one point. This means that the solution when you equate the two equations only has one value. So first, you substitute the equations

Kx = 3x2 -12x + 17
0 = 3x2 - (12+k)x +17

If you remember from secondary school, using the quadratic formula, if the determinant D is 0, that means the equation only has one solution.

D = b^2 -4ac
0 = (-12-k)^2 - 4(3)(17)
0 = 144 + 24k + k^2 - 204
0= k^2 + 24k - 60

This is the final quadratic equation. Solve for k, and then the negative value will be your answer.

Sorry it's so long but this is just my approach. You could probably think of a nicer one. Give it a try. Hope it helps!!!!