2)
Make use of:
Sum of arithmetic series
Set inclusion-exclusion principle

Want to pick integers that satisfy both:
NOT multiple of 7
and
NOT multiple of 11

e.g. Shouldn't pick 700, shouldn't pick 550, shouldn't pick 770

Can use set inclusion-exclusion principle
7 and 11 have no common factors
i.e. multiples of BOTH if and only if multiples of 77
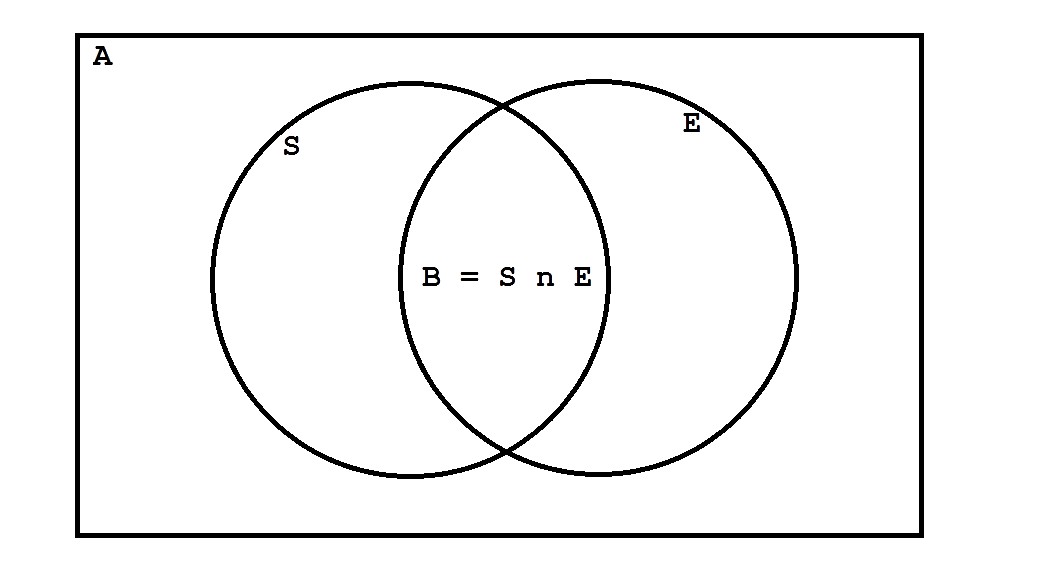
All integers in range A = {500, 501, 502, ..., 999, 1000}
Multiples of 7 in range S = {504, 511, 518, ..., 987, 994}
Multiples of 11 in range E = {506, 517, 528, ..., 979, 990}
Multiples of both 7 and 11 in range B = {539, 616, 693, ..., 847, 924}

Can find sum of all elements in each of A, S, E, B using arithmetic series
Common differences in each series are 1, 7, 11, 77 respectively

Answer = sum_A - sum_S - sum_E + sum_B
You take the universe and subtract the two circles (sets S and E)
But that removes the intersection twice, so you have to add the intersection back once (set B)
That gives you sum of numbers within 500...1000
with multiples of 7 removed, multiples of 11 removed
but takes care of multiples of 77 properly