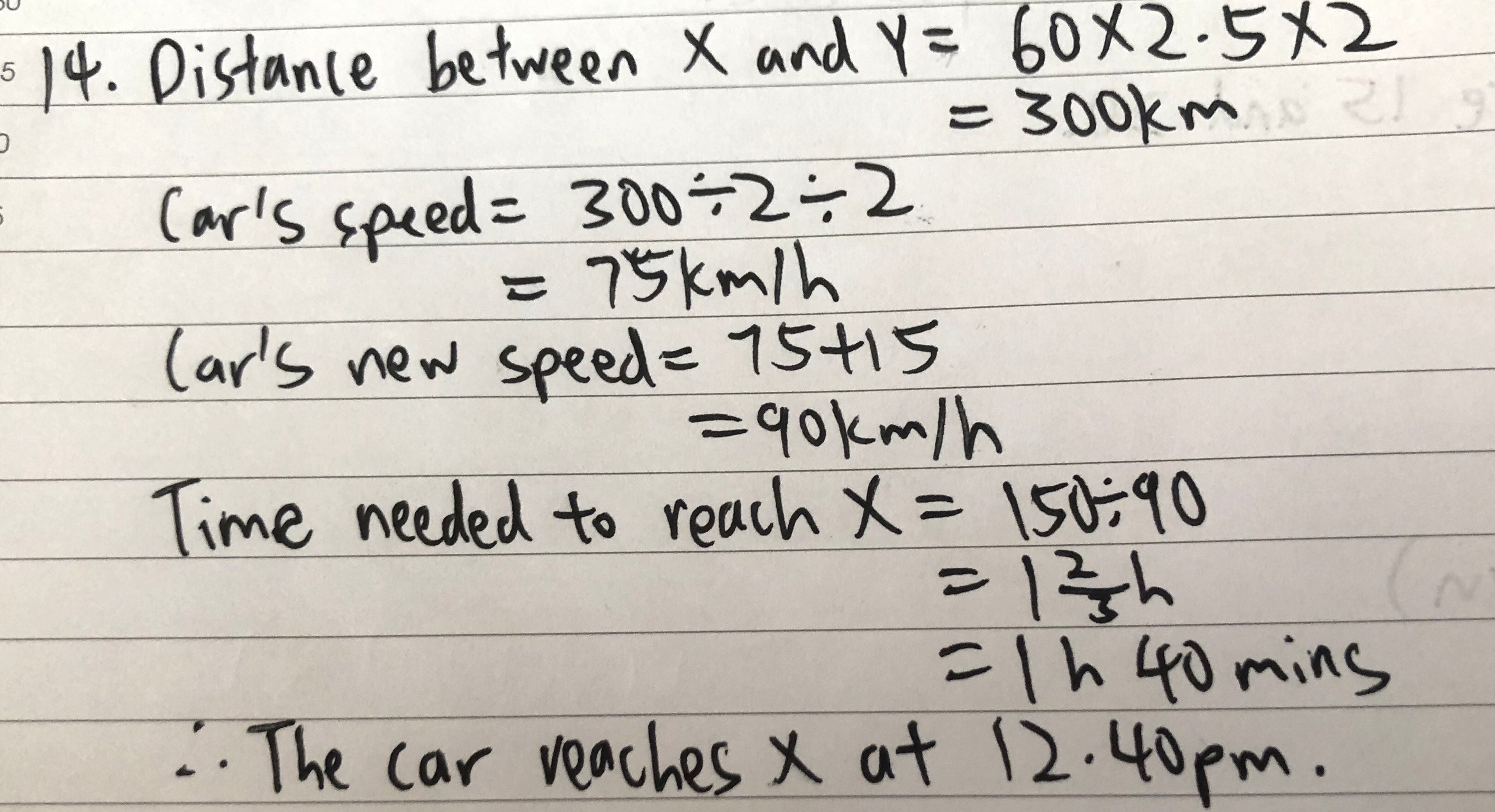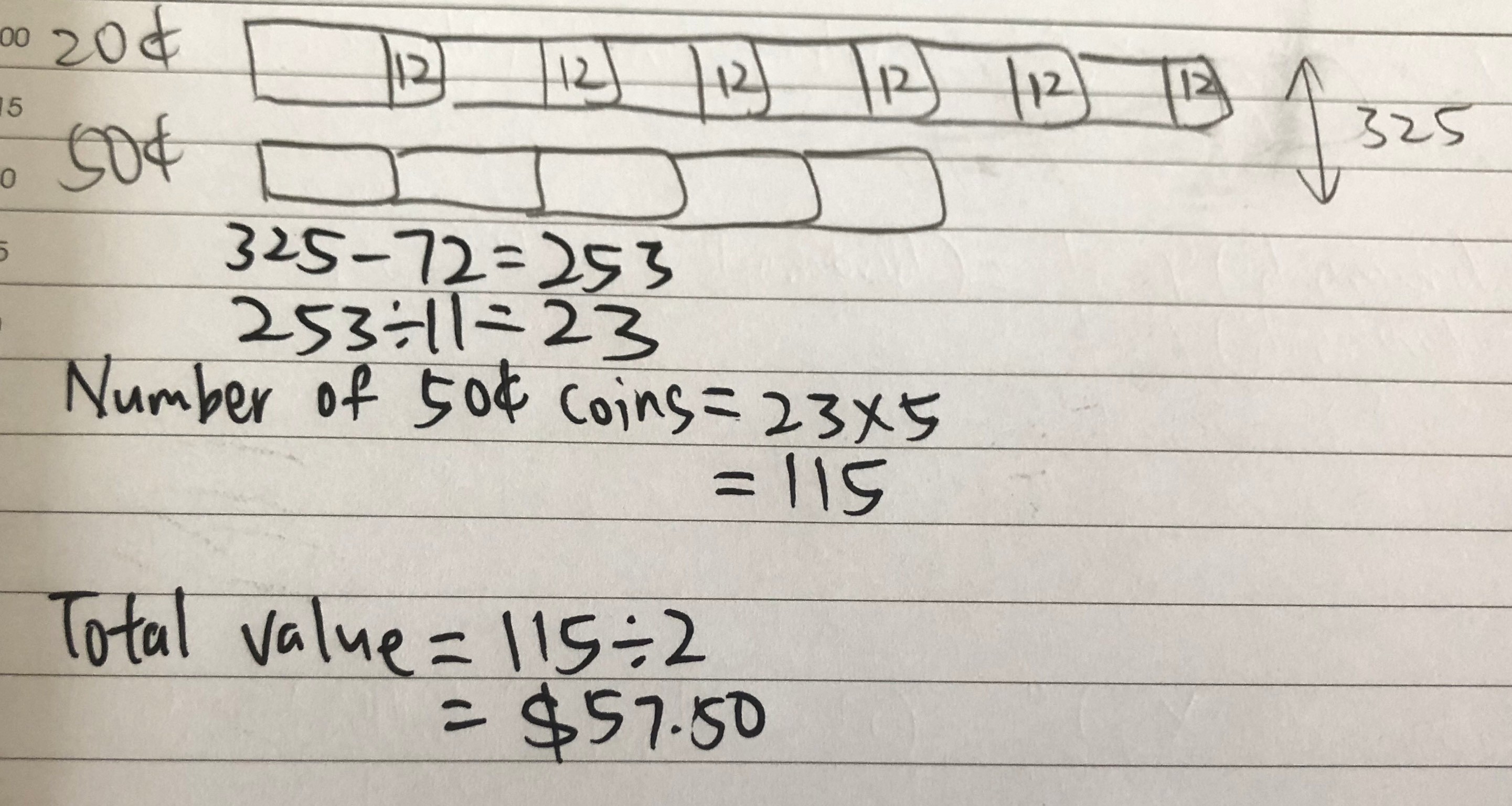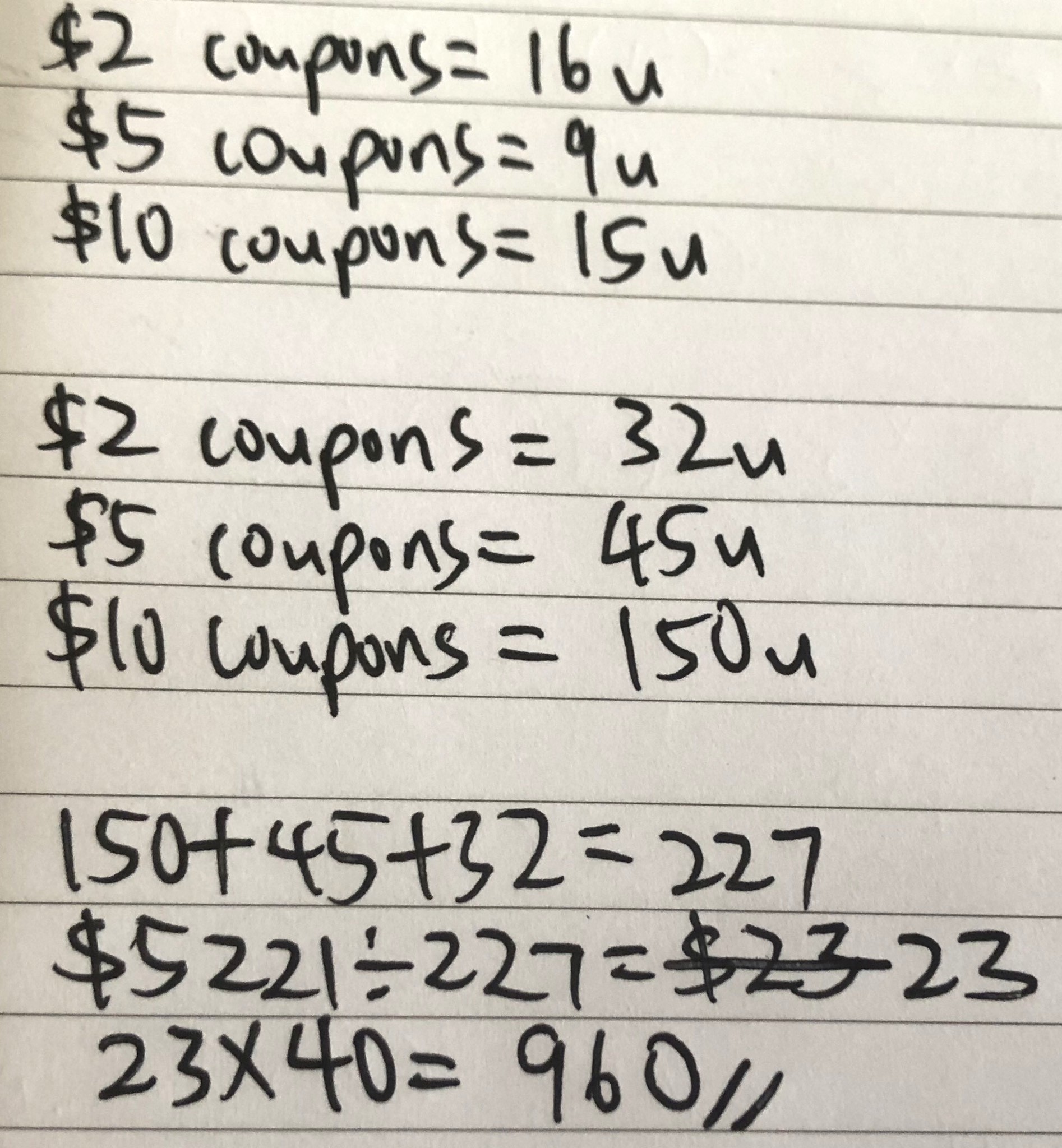For the first question, now the trick is here that u will realise that the lorry takes 2.5h to reach the midpoint between X and Y, so to get the total distance between X and Y, just remember to multiply by 2. Once we get the total distance, we can find out the car's original speed. The time taken for the car to reach the midpoint is 2h since it starts moving at 9am and met the lorry at 11am at midpoint. Remember to increment the car's speed after that then find the time taken to travel half of the total distance between X and Y and you are done

For this question, it is best to draw out the model and start with 1 unit first. So for 1 unit, 20 cent coin has 12 more than 1 unit of 50 cent coin. Once we establish this, we just draw the same unit 6 times for 20 cent coins and 5 times for 50 cent coins. Remember to replicate the 12 too as 1 unit + 12 is considered 1 unit for 20 cent coins. Once we have the model, the rest i believe it is easy for you.

For this question, take note that we have to change the fractions 2/5 and 3/8 as there are 3 units for remainder but 3/8 fraction indicates that there are 8 units for remainder so we must make 3 and 8 the same, so we have to multiply 2/5 by 8 for both numerator and denominator to get 16/40 and 3/8 by 3 to get 9/24 and so, the first 3 lines shows how many units each type of coupon actually has. There are too many units so i did not draw them but if u really cannot see, try drawing it out on your own.

Then now, the problem is each coupon is not $1, so to get the number of units in terms of $, we multiply the coupon by its value accordingly, so $2 coupon must times 2 and so on. This is so that we are able to get the ratio of the corresponding values of the coupons compared to one another. For the first 3 lines, the ratio is in terms of the number of coupons and for the next 3 lines, the ratio is in terms of the total value of each type of coupon.

Lastly, the $5221 is for the 2nd ratio since it is in terms of $. Then, to get the total number, just multiply the total number of units for the first ratio. Now take note that for the second ratio, i am just multiplying the first ratio by some constants so the units for both ratios are actually the same. Of course if u don't think so, u can manually calculate the value of each coupon, then divide by the value to get the number of coupons then add up all 3, you will still get 960 (: