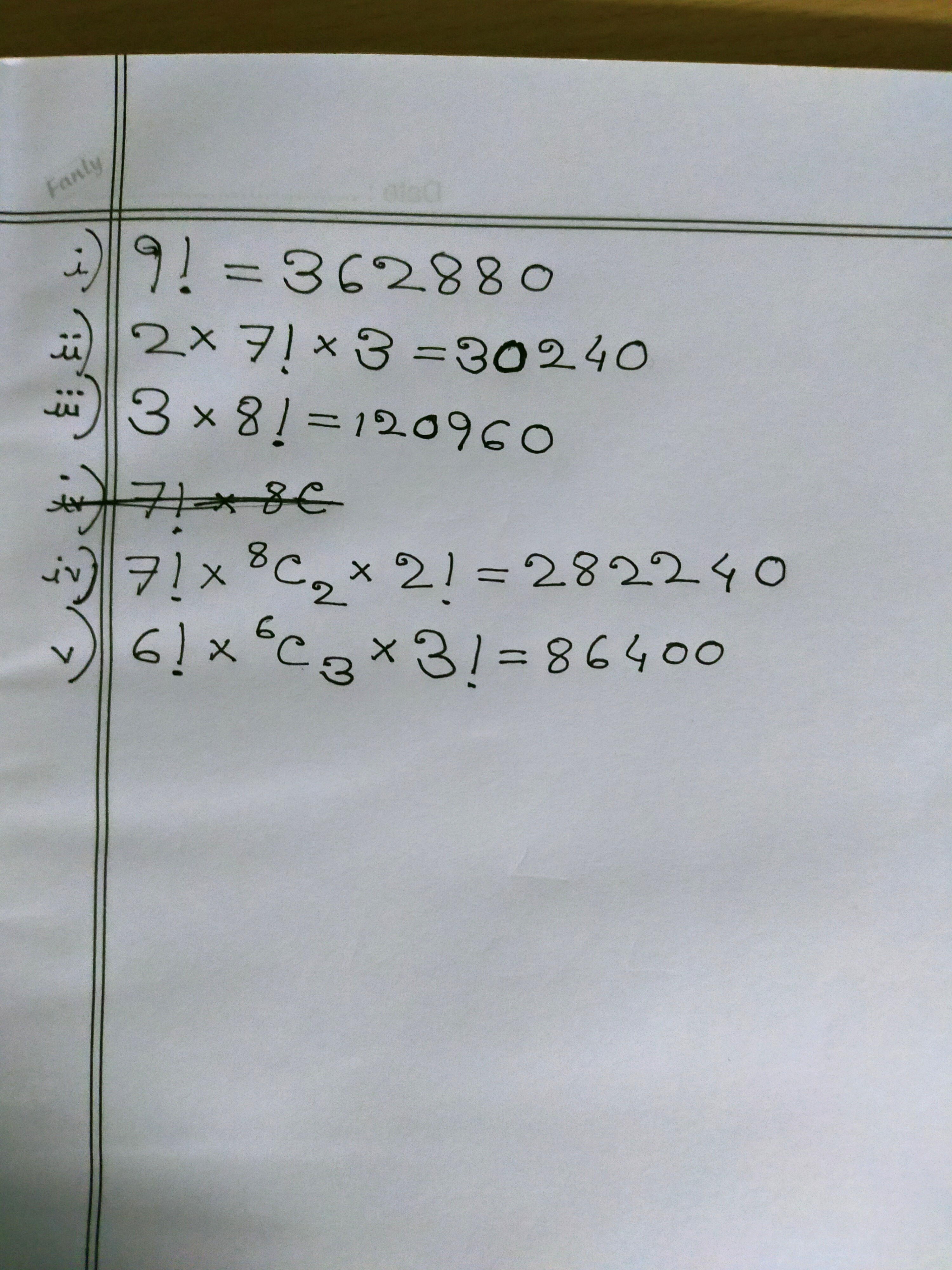Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
junior college 1 | H1 Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Thanks
a objects are type I,
b objects are type II,
c objects are type III.
total ways = n!/(a!b!c!)
(i)
among the 9 letters, there are ...
2 identical 'S' ; 2 identical 'I' ; 3 identical 'T' .
total ways = 9!/(2!2!3!) = 15120
(ii)
to place an 'S' at the beginning, there are 2 'S' that we can choose from, but both are identical, so effectively, it is considered only 1 way.
similarly, only 1 way to place a 'T' at the end.
after placing 'S' at beginning & 'T' at end, there are 7 remaining letters, which includes ...
2 identical 'T' & 2 identical 'I',
total ways = 1 x [7!/(2!2!)] x 1 = 1260
(iii)
have to split to 2 cases b'coz choice of 'A' or 'I' for 1st letter affects no. of ways to arrange remaining letters.
case I : 1st letter is vowel 'A'
there are 8 remaining letters, which includes ...
2 identical 'S', 2 identical 'I', 3 identical 'T' .
ways = 1 x [8!/(2!2!3!)] = 1680
case II : 1st letter is vowel 'I'
there are 8 remaining letters, which includes ...
2 identical 'S', 3 identical 'T' .
ways = 1 x [8!/(2!3!)] = 3360
total ways = 1680 + 3360 =5040
(iv)
use "grouping" method ...
bundle the 2 'S' together,
there are 7 remaining letters, which includes ...
2 identical 'I', 3 identical 'T'
7 remaining letters + 1 bundle of 'S' = 8 entities
total ways = 8!/(2!3!) = 3360
(v)
use "slotting" method ...
firstly, remove the 2 'S'
there are 7 remaining letters, which includes ...
2 identical 'I', 3 identical 'T'
ways to arrange the 7 remaining letters
= 7!/(2!3!) = 420
including the 2 ends, there are 8 slots for the 2 'S'.
ways to place the 2 'S' in 8 slots = 8C2 = 28
total ways = 420 x 28 = 11760
(vi)
use "slotting" method ...
firstly, remove the 3 'T'
there are 6 remaining letters, which includes ...
2 identical 'I', 2 identical 'S'
ways to arrange the 6 remaining letters
= 6!/(2!2!) = 180
including the 2 ends, there are 7 slots for the 3 'T'.
ways to place the 3 'T' in 7 slots = 7C3 = 35
total ways = 180 x 35 = 6300
See 1 Answer