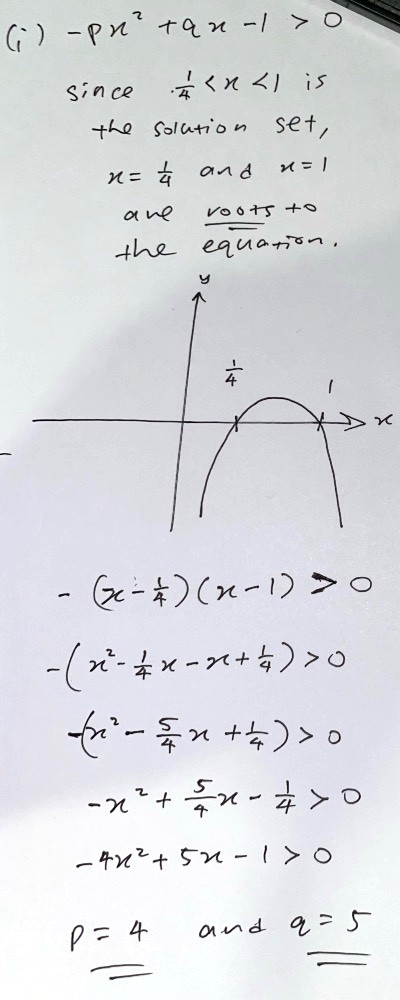Ask Singapore Homework?
Upload a photo of a Singapore homework and someone will email you the solution for free.

Question
secondary 3 | A Maths
One Answer Below
Anyone can contribute an answer, even non-tutors.

Inequalities
Date Posted: 1 year ago
Views: 298
A backward approach is usually applied here.
0.25 < x < 1
(x - 0.25) (x - 1) < 0
[Think why this is the case]
4 (x - 0.25) (x - 1) < 4 (0)
(4x - 1) (x - 1) < 0
4x² - 4x - x + 1 < 0
4x² - 5x + 1 < 0
-1 (4x² - 5x + 1) > -1 (0)
-4x² + 5x - 1 > 0
Check that the "-1" is satisfied in the equation
-px² + qx - 1 > 0.
0.25 < x < 1
(x - 0.25) (x - 1) < 0
[Think why this is the case]
4 (x - 0.25) (x - 1) < 4 (0)
(4x - 1) (x - 1) < 0
4x² - 4x - x + 1 < 0
4x² - 5x + 1 < 0
-1 (4x² - 5x + 1) > -1 (0)
-4x² + 5x - 1 > 0
Check that the "-1" is satisfied in the equation
-px² + qx - 1 > 0.
For part (b),
-px² + qx - 1 < 1 - 4x
[The less than here is to denote that the curve is below the line, or more precisely, the y-values of the curve are lower than the y-values of the line for a certain range of values of x]
-4x² + 5x - 1 < 1 - 4x
-4x² + 9x - 2 < 0
-1 (-4x² + 9x - 2) > -1 (0)
4x² - 9x + 2 > 0
(4x - 1) (x - 2) > 0
Solving, x < 1/4 or x > 2.
-px² + qx - 1 < 1 - 4x
[The less than here is to denote that the curve is below the line, or more precisely, the y-values of the curve are lower than the y-values of the line for a certain range of values of x]
-4x² + 5x - 1 < 1 - 4x
-4x² + 9x - 2 < 0
-1 (-4x² + 9x - 2) > -1 (0)
4x² - 9x + 2 > 0
(4x - 1) (x - 2) > 0
Solving, x < 1/4 or x > 2.
I can understand 0.25
If you have been solving inequalities for some time, (x - a) (x - b) < 0 <===> a < x < b.
This is because a “smiley face curve” with two x-intercepts works in such a way that the portion of the graph between the two x-intercepts is below the graph. The “less than zero” indicates this scenario.
The reverse will then be true.
If you are uncertain about this, you can always substitute random values of x to confirm this.
This is because a “smiley face curve” with two x-intercepts works in such a way that the portion of the graph between the two x-intercepts is below the graph. The “less than zero” indicates this scenario.
The reverse will then be true.
If you are uncertain about this, you can always substitute random values of x to confirm this.
See 1 Answer
done
{{ upvoteCount }} Upvotes
clear
{{ downvoteCount * -1 }} Downvotes
“ y = -px^2 + q -1 “ is the equation of a curve ( the graph i drew).
So, when they say the curve> 0, they are referring to the part of the curve that is positive, which is the part of the curve that is above the x-axis.
When they say the solutions to the equation is 1/4
So, when they say the curve> 0, they are referring to the part of the curve that is positive, which is the part of the curve that is above the x-axis.
When they say the solutions to the equation is 1/4
Date Posted:
1 year ago